Bài 1 trang 68 Toán 7 Cánh Diều tập 2
Câu hỏi
Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.
a) \( - 7x + 5\);
b) \(2021{x^2} - 2022x + 2023\);
c) \(2{y^3} - \dfrac{3}{{y + 2}} + 4\);
d) \( - 2{t^m} + 8{t^2} + t - 1\), với m là số tự nhiên lớn hơn 2.
Bài giải
Đa thức một biến là:
a) \( - 7x + 5\): biến của đa thức là x và bậc của đa thức là 1.
b) \(2021{x^2} - 2022x + 2023\): biến của đa thức là x và bậc của đa thức là 2
d) \( - 2{t^m} + 8{t^2} + t - 1\), với m là số tự nhiên lớn hơn 2: biến của đa thức là t và bậc của đa thức là m.
Bài 2 trang 68 Toán 7 Cánh Diều tập 2
Câu hỏi
Tính giá trị của biểu thức:
a) \(A = - 5a - b - 20\)tại \(a = - 4,b = 18\);
b) \(B = - 8xyz + 2xy + 16y\)tại \(x = - 1,y = 3,z = - 2\);
c) \(C = - {x^{2021}}{y^2} + 9{x^{2021}}\) tại \(x = - 2,y = - 3\).
Bài giải
a) Thay \(a = - 4,b = 18\)vào đa thức ta có:
\(A = - 5a - b - 20 = - 5. - 4 - 18 - 20 = - 18\).
b) Thay \(x = - 1,y = 3,z = - 2\)vào đa thức ta có:
\(B = - 8xyz + 2xy + 16y = - 8. - 1.3. - 2 + 2. - 1.3 + 16.3 = - 48 - 6 + 48 = - 6\)
.c) Thay \(x = - 2,y = - 3\)vào đa thức ta có:
\(C = - {x^{2021}}{y^2} + 9{x^{2021}} = - {( - 1)^{2021}}.{( - 3)^2} + 9.{( - 1)^{2021}} = - ( - 1).9 + 9.( - 1) = 9 + ( - 9) = 0\).
Bài 3 trang 68 Toán 7 Cánh Diều tập 2
Câu hỏi
Viết đa thức trong mỗi trường hợp sau:
a) Đa thức bậc nhất có hệ số của biến bằng – 2 và hệ số tự do bằng 6;
b) Đa thức bậc hai có hệ số tự do bằng 4;
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.
Bài giải
a) Đa thức bậc nhất có hệ số của biến bằng – 2 và hệ số tự do bằng 6 tức \(a = - 2;b = 6\)
\( - 2x + 6\).
b) Đa thức bậc hai có hệ số tự do bằng 4: \({x^2} + x + 4\).
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0: \({x^4} + 0.{x^3} + {x^2} + 1 = {x^4} + {x^2} + 1\).
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0: \({x^6} + 0.{x^5} + {x^4} + 0.{x^3} + {x^2} + 0.x = {x^6} + {x^4} + {x^2}\).
Bài 4 trang 68 Toán 7 Cánh Diều tập 2
Câu hỏi
Kiểm tra xem trong các số – 1, 0, 1, 2, số nào là nghiệm của mỗi đa thức sau:
a) \(3x - 6\);
b) \({x^4} - 1\);
c) \(3{x^2} - 4x\);
d) \({x^2} + 9\).
Bài giải
a) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}3.( - 1) - 6 = - 3 - 6 = - 9\\3.0 - 6 = 0 - 6 = - 6\\3.1 - 6 = 3 - 6 = - 3\\3.2 - 6 = 6 - 6 = 0\end{array}\)
Vậy 2 là nghiệm của đa thức \(3x - 6\).
b) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}{( - 1)^4} - 1 = 1 - 1 = 0\\{0^4} - 1 = 0 - 1 = - 1\\{1^4} - 1 = 1 - 1 = 0\\{2^4} - 1 = 16 - 1 = 15\end{array}\)
Vậy 1 và – 1 là nghiệm của đa thức \({x^4} - 1\)
c) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}3.{( - 1)^2} - 4.( - 1) = 3 + 4 = 7\\{3.0^2} - 4.0 = 0 - 0 = 0\\{3.1^2} - 4.1 = 3 - 4 = - 1\\{3.2^2} - 4.2 = 12 - 8 = 4\end{array}\)
Vậy 0 là nghiệm của đa thức \(3{x^2} - 4x\).
d) Thay các giá trị – 1, 0, 1, 2 vào biểu thức ta được:
\(\begin{array}{l}{( - 1)^2} + 9 = 1 + 9 = 10\\{0^2} + 9 = 0 + 9 = 9\\{1^2} + 9 = 1 + 9 = 10\\{2^2} + 9 = 4 + 9 = 13\end{array}\)
Vậy không giá trị nào là nghiệm của đa thức \({x^2} + 9\).
Bài 5 trang 68 Toán 7 Cánh Diều tập 2
Câu hỏi
Cho đa thức \(P(x) = - 9{x^6} + 4x + 3{x^5} + 5x + 9{x^6} - 1\).
a) Thu gọn đa thức P(x).
b) Tìm bậc của đa thức P(x).
c) Tính giá trị của đa thức P(x) tại \(x = - 1;x = 0;x = 1\).
Bài giải
a) \(\begin{array}{l}P(x) = - 9{x^6} + 4x + 3{x^5} + 5x + 9{x^6} - 1 = ( - 9{x^6} + 9{x^6}) + 3{x^5} + (4x + 5x) - 1\\ = 0 + 3{x^5} + 9x - 1 = 3{x^5} + 9x - 1\end{array}\).
b) Bậc của đa thức là 5.
c) Thay \(x = - 1;x = 0;x = 1\) vào đa thức ta được:
\(\begin{array}{l}P( - 1) = 3.{( - 1)^5} + 9.( - 1) - 1 = 3.( - 1) - 9 - 1 = - 3 - 9 - 1 = - 13.\\P(0) = {3.0^5} + 9.0 - 1 = 3.0 - 1 = 0 - 1 = - 1.\\P(1) = {3.1^5} + 9.1 - 1 = 3.1 + 9 - 1 = 3 + 9 - 1 = 11.\end{array}\)
Bài 6 trang 68 Toán 7 Cánh Diều tập 2
Câu hỏi
Tính:
a) \( - 2{x^2} + 6{x^2}\);
b) \(4{x^3} - 8{x^3}\);
c) \(3{x^4}( - 6{x^2})\);
d) \(( - 24{x^6}):( - 4{x^3})\).
Bài giải
a) \( - 2{x^2} + 6{x^2} = ( - 2 + 6).{x^2} = 4{x^2}\);
b) \(4{x^3} - 8{x^3} = (4 - 8).{x^3} = - 4{x^3}\);
c) \(3{x^4}( - 6{x^2}) = 3.( - 6).{x^4}.{x^2} = - 18{x^{4 + 2}} = - 18{x^6}\);
d) \(( - 24{x^6}):( - 4{x^3}) = ( - 24: - 4).({x^6}:{x^3}) = 6{x^{6 - 3}} = 6{x^3}\).
Bài 7 trang 68 Toán 7 Cánh Diều tập 2
Câu hỏi
Tính:
a) \(({x^2} + 2x + 3) + (3{x^2} - 5x + 1)\);
b) \((4{x^3} - 2{x^2} - 6) - ({x^3} - 7{x^2} + x - 5)\);
c) \( - 3{x^2}(6{x^2} - 8x + 1)\);
d) \((4{x^2} + 2x + 1)(2x - 1)\);
e) \(({x^6} - 2{x^4} + {x^2}):( - 2{x^2})\);
g) \(({x^5} - {x^4} - 2{x^3}):({x^2} + x)\).
Bài giải
a) \(({x^2} + 2x + 3) + (3{x^2} - 5x + 1) = ({x^2} + 3{x^2}) + (2x - 5x) + (3 + 1) = 4{x^2} - 3x + 4\);
b) \(\begin{array}{l}(4{x^3} - 2{x^2} - 6) - ({x^3} - 7{x^2} + x - 5) = 4{x^3} - 2{x^2} - 6 - {x^3} + 7{x^2} - x + 5\\ = (4{x^3} - {x^3}) + ( - 2{x^2} + 7{x^2}) - x + ( - 6 + 5) = 3{x^3} + 5{x^2} - x - 1\end{array}\);
c) \(\begin{array}{l} - 3{x^2}(6{x^2} - 8x + 1) = - 3{x^2}.6{x^2} - - 3{x^2}.8x + - 3{x^2}.1\\ = - 18{x^{2 + 2}} + 24{x^{2 + 1}} - 3{x^2} = - 18{x^4} + 24{x^3} - 3{x^2}\end{array}\);
d) \(\begin{array}{l}(4{x^2} + 2x + 1)(2x - 1) = (4{x^2} + 2x + 1).2x - (4{x^2} + 2x + 1).1 = 4{x^2}.2x + 2x.2x + 1.2x - 4{x^2} - 2x - 1\\ = 8{x^{2 + 1}} + 4{x^{1 + 1}} + 2x - 4{x^2} - 2x - 1 = 8{x^3} + 4{x^2} + 2x - 4{x^2} - 2x - 1 = 8{x^3} - 1\end{array}\);
e) \(\begin{array}{l}({x^6} - 2{x^4} + {x^2}):( - 2{x^2}) = {x^6}:( - 2{x^2}) - 2{x^4}:( - 2{x^2}) + {x^2}:( - 2{x^2})\\ = - \dfrac{1}{2}{x^{6 - 2}} + {x^{4 - 2}} - \dfrac{1}{2}{x^{2 - 2}} = - \dfrac{1}{2}{x^4} + {x^2} - \dfrac{1}{2}.\end{array}\);
g)
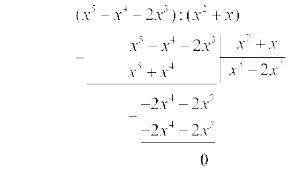
\(({x^5} - {x^4} - 2{x^3}):({x^2} + x)=x^3-2x^2\)
Bài tiếp theo: |
Xem thêm:
Trên đây là chi tiết hướng dẫn Giải bài tập Toán 7 Cánh Diều trang 68 được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Cánh Diều bởi Đọc Tài Liệu