Trong chương trình Toán lớp 9, các em sẽ được làm quen với tiếp tuyến. Đây là phần kiến thức quan trọng, những dạng toán về tiếp tuyến sẽ xuất hiện trong hầu hết các bài thi quan trọng ở các mức độ khác nhau từ dễ đến khó.
Để các em nắm được đầy đủ kiến thức về phần này, Đọc Tài Liệu đem đến tài liệu tổng hợp lý thuyết tính chất của hai tiếp tuyến cắt nhau ở bài viết dưới đây, hy vọng sẽ là một tài liệu hữu ích cho quá trình học tập của các em.
Cùng tham khảo nhé!

I. Lý thuyết về tính chất của hai tiếp tuyến cắt nhau
a. Tính chất hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Nghĩa là cho đường tròn \(\left( O \right), B,C \in \left( O \right)\). Tiếp tuyến của \(\left( O \right)\) tại B,C cắt nhau tại A.
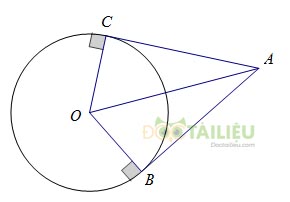
Khi đó
- AB = AC
- Tia OC là phân giác góc \(\widehat {BOC}\)
- Tia AO là phân giác góc \(\widehat {BAC}\)
b. Đường tròn nội tiếp tam giác
Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác các góc trong tam giác.
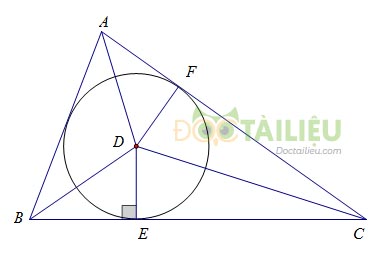
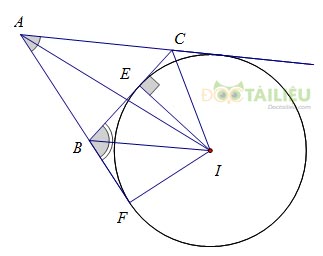
c. Đường tròn bàng tiếp tam giác
- Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dàicủa hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.
- Với một tam giác có ba đường tròn bàng tiếp.
Ví dụ: Xét tam giác ABC, tâm của đường tròn bàng tiếp tam giác góc A là giao điểm của hai đường phân giác ngoài tại B, C, hoặc là giao điểm của đường phân giác trong góc A và đường phân giác ngoài tại B (hoặc C).
II. Các dạng toán thường gặp về tính chất của hai tiếp tuyến cắt nhau
Dạng 1: Chứng minh các đường thẳng song song (vuông góc), chứng minh hai đoạn thẳng bằng nhau.
Phương pháp:
Dùng tính chất của hai tiếp tuyến cắt nhau.
Dạng 2: Chứng minh một đường thẳng là tiếp tuyến, tính độ dài, số đo góc và các yếu tố khác.
Phương pháp:
- Dùng định nghĩa tiếp tuyến; tính chất của hai tiếp tuyến cắt nhau.
- Dùng khái niệm đường tròn nội tiếp, bàng tiếp.
- Dùng hệ thức lượng về cạnh và góc trong tam giác vuông.
III. Bài tập về tính chất của hai tiếp tuyến cắt nhau
Cho đường tròn (I) nội tiếp tam giác ABC. Các tiếp điểm trên AC, AB theo thứ tự là D, E. Cho BC = a, AC = b, AB = c. Tính độ dài các đoạn tiếp tuyến AD, AE theo a, b, c.
Lời giải:
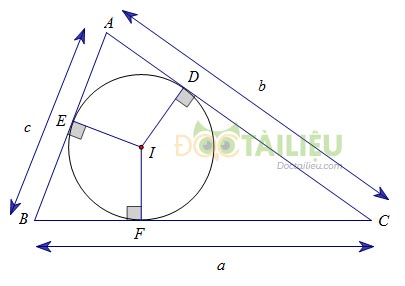
Gọi F là tiếp điểm của đường tròn (I) với BC.
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
AE = AD
BE = BF
CD = CF
Mà: AE = AB – BE
AD = AC – CD
Nên: AE + AD = (AB –BE) + (AC – CD)
= AB + AC – (BE + CD)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra: AE + AD = c + b – a
Hay: \(AE = AD =\displaystyle {{c + b - a} \over 2}\)
=>> Xem thêm nhiều bài tập khác trong chuyên đề toán hình 9 chương 2 bài 6 để củng cố kiến thức và rèn luyện kỹ năng làm bài
********************
Hy vọng với hệ thống kiến thức lý thuyết tính chất của hai tiếp tuyến cắt nhau trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!