Những nội dung của bài viết này sẽ giúp các em ôn tập và nắm vững kiến thức lý thuyết tỉ lệ bản đồ và ứng dụng của tỉ lệ bản đồ nằm trong chương trình học môn Toán lớp 4.
Tỉ lệ bản đồ là gì?
Tỉ lệ bản đồ là tỉ số giữa một khoảng cách đo trên bản đồ và khoảng cách ngoài thực địa. Trên mỗi bản đồ, tỉ lệ được đặt ở dưới tên bản đồ cho người đọc biết được mức độ thu nhỏ của đối tượng ngoài thực tế lên bản đồ.
- Tỉ lệ bản đồ có thể viết dưới dạng một phân số có tử số là \(1\).
Ví dụ: \(\dfrac{1}{{1000}}\,\,\,\,\,\,;\,\,\,\,\,\,\,\dfrac{1}{{500}}\,\,\,\,\,\,;\,\,\,\,\,\,\,\dfrac{1}{{1\,\,000\,\,000}}\)
Thước tỉ lệ thường đặt ở dưới góc bản đồ phục vụ cho việc đo đạc các thông số như khoảng cách và diện tích trên bản đồ.
Ví dụ tỉ lệ bản đồ
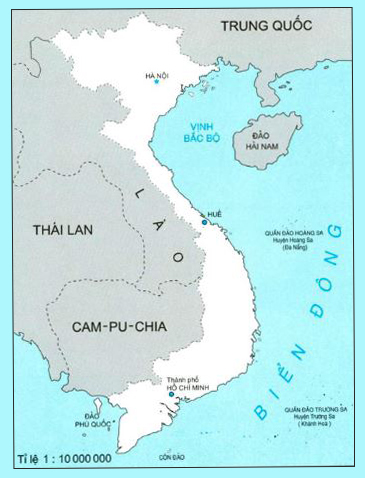
Ở góc phía dưới của bản đồ nước Việt Nam có ghi: Tỉ lệ \(1:\,\,10\,\,000\,\,000\). Tỉ lệ đó là tỉ lệ bản đồ.
- Tỉ lệ \(1:\,\,10\,\,000\,\,000\) hay \(\dfrac{1}{{10\,\,000\,\,000}}\) cho biết hình nước Việt Nam được vẽ thu nhỏ lại \(10\,\,000\,\,000\) lần. Chẳng hạn: độ dài \(1cm\) trên bản đồ ứng với độ dài thật là \(10\,\,000\,\,000cm\) hay \(100km\)
Ứng dụng của tỉ lệ bản đồ
Ứng dụng của tỉ lệ bản đồ gồm:
- Tính độ dài thật
- Tính độ dài thu nhỏ trên bản đồ
Tính độ dài thật
Bài toán
Bản đồ trường Mầm non xã Thắng Lợi vẽ theo tỉ lệ \(1:300\).
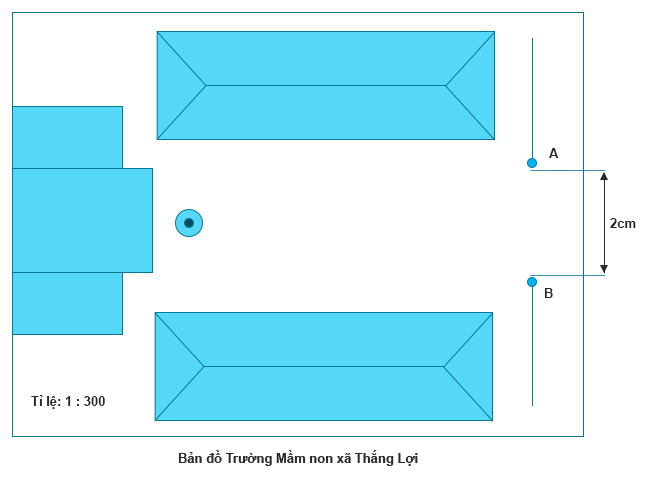
Trên bản đồ, cổng trường rộng \(2cm\) (khoảng cách từ A đến B). Hỏi chiều rộng thật của cổng trường là mấy mét?
Giải:
Chiều dài thật của cổng trường là:
\(\begin{array}{l}2 \times 300 = 600\,\,(cm)\\600cm = 6m\end{array}\)
Đáp số: \(6m\)
Tính độ dài thu nhỏ trên bản đồ
Bài toán
Khoảng cách giữa hai điểm A và B trên sân trường là \(20m\). Trên bản đồ tỉ lệ \(1:500\), khoảng cách giữa hai điểm đó là mấy xăng-ti-mét?
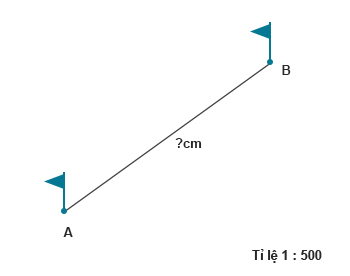
Bài giải
\(20m = 2000cm\)
Khoảng cách giữa hai điểm A và B trên bản đồ là:
\(2000:500 = 4\,\,(cm)\)
Đáp số: \(4cm\)
Tham khảo thêm tài liệu hướng dẫn giải toán 4 trang 155 bài tỉ lệ bản đồ trong sách giáo khoa
Trên đây là lý thuyết bài học Tỉ lệ bản đồ và ứng dụng của tỉ lệ bản đồ đã được Đọc Tài Liệu biên soạn để giúp các em ôn tập. Chúc các em luôn đạt kết quả cao trong học tập.