Trong chương trình Toán lớp 9, các em sẽ được làm quen với hình trụ. Đây là phần kiến thức quan trọng, những dạng toán về hình trụ sẽ xuất hiện trong hầu hết các bài thi quan trọng ở các mức độ khác nhau từ dễ đến khó.
Để các em nắm được đầy đủ kiến thức về phần này, Đọc Tài Liệu đem đến tài liệu tổng hợp lý thuyết Hình trụ - Diện tích xung quanh và thể tích hình trụ ở bài viết dưới đây, hy vọng sẽ là một tài liệu hữu ích cho quá trình học tập của các em.
Cùng tham khảo nhé!

I. Lý thuyết Hình trụ - Diện tích xung quanh và thể tích hình trụ
1. Hình trụ
Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định ta thu được một hình trụ.
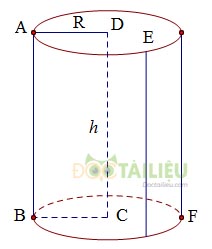
- Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.
- DC là trục của hình trụ.
- Các đường sinh của hình trụ ( chẳng hạn EF) vuông góc với hai mặt đáy.
Độ dài đường sinh cũng là độ dài đường cao của hình trụ.
2. Diện tích xung quanh của hình trụ:
Hình trụ có r là bán kính đường tròn đáy, h là chiều cao thì có
Diện tích xung quanh là: \({S_{xq}} = 2πrh\)
Diện tích 2 đáy là: \( S_{2đáy}=2 \pi r^2 \)
Diện tích toàn phần là: \( {S_{tp}} = 2πrh + 2πr^2\)
3. Thể tích hình trụ
Công thức tính thể tích hình trụ: \(V= Sh = πr^2h\)
(S là diện tích đáy, h: là chiều cao)
II. Các dạng toán thường gặp về Hình trụ - Diện tích xung quanh và thể tích hình trụ
Dạng 1: Tính bán kính đáy, chiều cao và diện tích xung quanh, diện tích toàn phần và thể tích hình trụ
Phương pháp:
Sử dụng các công thức tính bán kính đáy, chiều cao, diện tích đáy, diện tích xung quanh, diện tích toàn phần và thể tích hình trụ.
+ Diện tích xung quanh : \({S_{xq}} = 2\pi Rh\)
+ Diện tích đáy : \({S_{d}}=\pi {R^2}\).
+ Diện tích toàn phần : \({S_{tp}} = {S_{xq}} + 2.{S_{d}} = 2\pi Rh + 2\pi {R^2}.\)
+ Thể tích : \(V = \pi {R^2}h\).
Dạng 2 : Bài tập tổng hợp
Phương pháp :
Sử dụng hệ thức lượng trong tam giác vuông và các công thức liên quan đến hình trụ.
III. Bài tập về Hình trụ - Diện tích xung quanh và thể tích hình trụ
Một hình trụ có bán kính đường tròn đáy là 6cm, chiều cao 9cm. Hãy tính:
a) Diện tích xung quanh của hình trụ.
b) Thể tích của hình trụ.
(Lấy \(\pi \approx 3,142\) làm tròn kết quả đến hàng đơn vị).
Lời giải:
a) Diện tích xung quanh hình trụ là:
\({S_{xq}}= 2πrh\)
\({S_{xq}} = 2.3,142.6.9 \approx 339\;(c{m^2})\)
b) Thể tích hình trụ là:
\(V= πr^2h\)
\(V = 3,{142.6^2}.9 \approx 1018\;(c{m^3}).\)
=>> Xem thêm nhiều bài tập khác trong Toán hình 9 chương 4 bài 1 để củng cố kiến thức và rèn luyện kỹ năng làm bài
****************
Hy vọng với hệ thống kiến thức lý thuyết Hình trụ - Diện tích xung quanh và thể tích hình trụ trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!