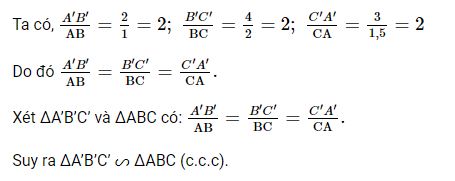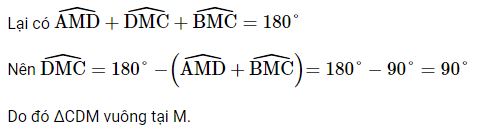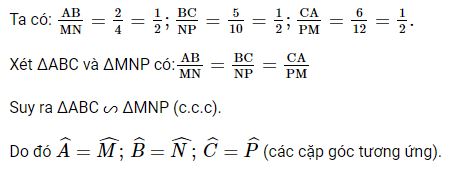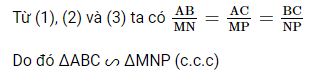Hướng dẫn trả lời câu hỏi và giải bài tập Toán 8 Cánh Diều tập 2 giúp học sinh nắm được các cách giải bài tập Chương 8: Ứng dụng của định lí Thalès trong tam giác chuẩn bị bài trước khi tới lớp và luyện tập giải toán tại nhà.
Chương 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Khởi động trang 74 Toán 8 Tập 2: Mảnh đất trồng hoa của nhà bạn Hằng có dạng hình tam giác với độ dài các cạnh là 2 m, 3 m, 4 m. Bạn Hằng vẽ tam giác ABC có độ dài các cạnh là 1 cm, 1,5 cm, 2 cm để mô tả hình ảnh mảnh vườn đó (Hình 56a). Bạn Khôi nói rằng tam giác ABC nhỏ quá và vẽ tam giác A’B’C’ có độ dài các cạnh là 2 cm, 3 cm, 4 cm (Hình 56b).Hai tam giác A’B’C’ và ABC có đồng dạng hay không?
Lời giải:
I. Trường hợp đồng dạng thứ nhất: Cạnh-cạnh-cạnh
Hoạt động 1 trang 74 Toán 8 Tập 2: Quan sát Hình 56 và so sánh các tỉ số \(\dfrac{A'B'}{AB}; \dfrac{A'C'}{AC}; \dfrac{B'C'}{BC}\).
Lời giải:
Ta có \(\dfrac{A'B'}{AB} = \dfrac{2}{1} = 2; \dfrac{B'C'}{BC} = \dfrac{4}{2} = 2; \dfrac{A'C'}{AC} = \dfrac{3}{1,5} = 2\)
Do đó: \(\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC} = \dfrac{A'C'}{AC}\).
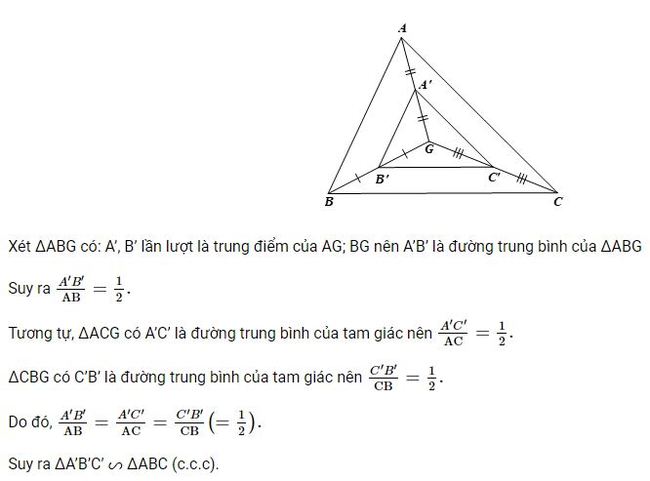
Luyện tập 1 trang 75 Toán 8 Tập 2: Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của AG; BG; CG. Chứng minh ∆A’B’C’ ᔕ ∆ABC.
Lời giải:
II. Áp dụng trường hợp đồng dạng thứ nhất của tam giác vào tam giác vuông
Hoạt động 2 trang 76 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ (Hình 60) sao cho AB = 3, BC = 5, A’B’ = 6, B’C’ = 10.
a) Tính CA và C’A’.
b) So sánh các tỉ số \(\dfrac{A'B'}{AB}; \dfrac{B'C'}{BC}; \dfrac{C'A'}{CA}\)
c) Hai tam giác A’B’C’ và ABC có đồng dạng với nhau hay không
Lời giải:
a) Xét ∆ABC vuông tại A, theo định lí Pythagore ta có:
\(BC^2 = AB^2 + AC^2\)
Suy ra \(AC^2 =BC^2 – AB^2 = 25 ‒ 9 =16\).
Do đó AC = 4.
Xét ∆A’B’C’ vuông tại A’, theo định lí Pythagore ta có:
\(B’C’^2 = A’B’^2 + A’C’^2\)
Suy ra \(A’C’^2 =B’C’^2 – A’B’^2 = 100 ‒ 36 = 64\)
Do đó A’C’ = 8.
b) Ta có: \(\dfrac{A'B'}{AB} = \dfrac{6}{3} = 2; \dfrac{B'C'}{BC} = \dfrac{10}{5} = 2; \dfrac{C'A'}{CA} = \dfrac{8}{4} = 2\).
Do đó: \(\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC} = \dfrac{C'A'}{CA}\)
Suy ra ∆A’B’C’ ᔕ ∆ABC (c.c.c).
Luyện tập 2 trang 78 Toán 8 Tập 2:
Cho Hình 64, chứng minh tam giác CDM vuông tại M.Lời giải:
Bài tập
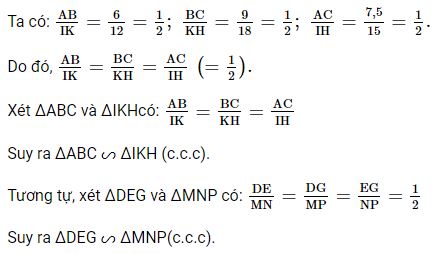
Bài 1 trang 78 Toán 8 Tập 2: Quan sát Hình 65 và chỉ ra những cặp tam giác đồng dạng:
Lời giải:
Bài 2 trang 78 Toán 8 Tập 2: Cho hai tam giác ABC và MNP có AB = 2; BC = 5; CA = 6; MN = 4; NP = 10; PM = 12. Hãy viết các cặp góc tương ứng bằng nhau của hai tam giác trên và giải thích kết quả.
Lời giải:
Bài 3 trang 78 Toán 8 Tập 2: Bác Hùng vẽ bản đồ trong đó dùng ba đỉnh A, B, C của tam giác ABC lần lượt mô tả ba vị trí M, N, P trong thực tiễn. Bác Duy cũng vẽ một bản đồ trong đó dùng ba đỉnh A’, B’, C’ của tam giác A’B’C’ lần lượt mô tả ba vị trí M, N, P đó. Tỉ lệ bản đồ mà bác Hùng và bác Duy vẽ lần lượt là 1 : 1 000 000 và 1 : 1 500 000. Chứng minh ∆ABC ᔕ ∆A’B’C’ và tính tỉ số đồng dạng.
Lời giải:
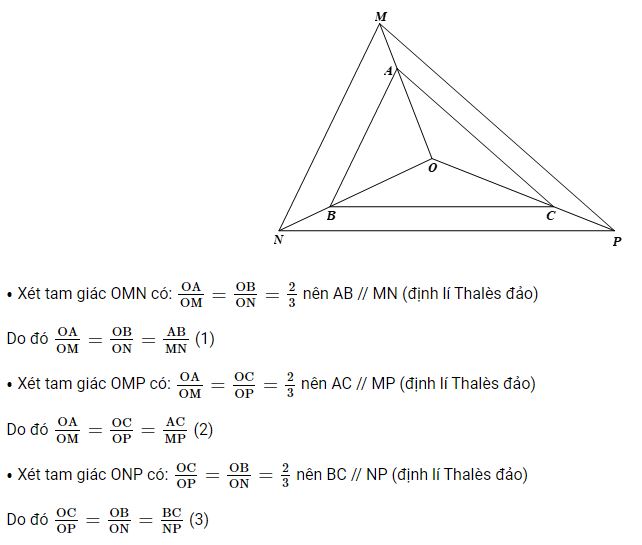
Bài 4 trang 78 Toán 8 Tập 2: Cho tam giác ABC và điểm O nằm trong tam giác. Các điểm M, N, P lần lượt thuộc tia OA, OB, OC sao cho \(\dfrac{OA}{OM} = \dfrac{OB}{ON} = \dfrac{OC}{OP} = \dfrac{2}{3}\)
.Chứng minh ∆ABC ᔕ ∆MNP.
Lời giải:
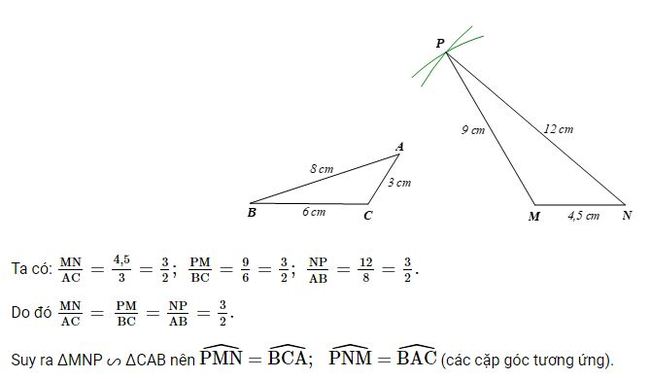
Bài 5 trang 78 Toán 8 Tập 2: Bạn Hoa vẽ trên giấy một tam giác ABC và đoạn thẳng MN với các kích thước như Hình 66. Bạn Hoa đố bạn Thanh vẽ điểm P thỏa mãn \(\widehat{PMN} = \widehat{ACB}; \widehat{PNM} = \widehat{BAC}\) mà không sử dụng thước đo góc. Em hãy giúp bạn Thanh sử dụng thước thẳng (có chia khoảng milimét) và compa để vẽ điểm P và giải thích kết quả tìm được.
Lời giải:
Bước 1. Qua M vẽ cung tròn tâm M, bán kính là 9 cm.
Bước 2.. Qua N, vẽ cung tròn tâm N, bán kính là 12 cm.
Bước 3. Giao điểm của hai cung tròn đã vẽ là điểm P.
Ta được: MP = 9 cm; NP = 12 cm.
Bài 6 trang 78 Toán 8 Tập 2: Cho hình bình hành ABCD và BMNP như ở Hình 67. Chứng minh:
a) \(\dfrac{BM}{BA} = \dfrac{BP}{BC}\);
b) ∆MNP ᔕ ∆CBA.
Lời giải:
-//-
Hy vọng với nội dung trả lời chi tiết câu hỏi trong Bài 6: Trường hợp đồng dạng thứ nhất của tam giác giúp học sinh nắm được nội dung bài học và ghi nhớ những nội dung chính, quan trọng trong chương trình học Toán học 8.