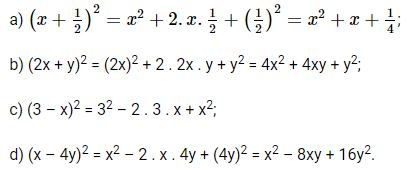Hướng dẫn trả lời câu hỏi và giải bài tập Toán 8 Cánh Diều tập 1 giúp học sinh nắm được các cách giải bài tập Chương 1: Đa thức nhiều biến chuẩn bị bài trước khi tới lớp và luyện tập giải toán tại nhà.
Chương 1 Bài 3: Hằng đẳng thức đáng nhớ
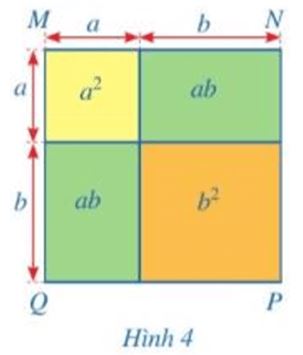
Khởi động trang 18 Toán 8 Tập 1: Diện tích của hình vuông MNPQ (Hình 4) có thể được tính theo những cách nào?
Lời giải:
Ta đặt tên các điểm A, B, C, D như hình vẽ:
Diện tích của hình vuông MNPQ có thể được tính theo những cách sau:
Cách 1. Tính theo tổng diện tích của 4 hình AMCE, ANDE, BEDP, BECQ.
Cách 2. Tính theo tổng diện tích của 2 hình: MNDC, CDPQ.
Cách 3. Tính theo tổng diện tích của 2 hình: ABQM, ABPN.
Cách 4. Tìm độ dài một cạnh của hình vuông MNPQ rồi tính diện tích.
Hoạt động 1 trang 18 Toán 8 Tập 1: Xét hai biểu thức: P = 2(x + y) và Q = 2x + 2y. Tính giá trị của mỗi biểu thức P và Q rồi so sánh hai giá trị đó trong mỗi trường hợp sau:
a) Tại x = 1; y = −1;
b) Tại x = 2; y = −3.
Lời giải:
a) Thay x = 1; y = −1 vào biểu thức P và Q, ta được:
- P = 2 . [1 + (−1)] = 2 . 0 = 0;
- Q = 2 . 1 + 2 . (−1) = 2 – 2 = 0.
Vậy tại x = 1; y = −1 thì P = Q.
b) Thay x = 2; y = −3 vào biểu thức P và Q, ta được:
- P = 2 . [2 + (−3)] = 2 . (−1) = −2;
- Q = 2 . 2 + 2 . (−3) = 4 – 6 = −2.
Vậy tại x = 2; y = −3 thì P = Q.
Luyện tập 1 trang 18 Toán 8 Tập 1: Chứng minh rằng: \(x(xy^2 + y) – y(x^2y + x) = 0\).
Lời giải:
Ta có \(x(xy^2 + y) – y(x^2y + x) = x . xy^2 + x . y – y . x^2y – y . x\)
\(= x^2y^2 + xy – x^2y^2 – xy = (x^2y^2 – x^2y^2) + (xy – xy) = 0 + 0 = 0\) (đpcm)
Hoạt động 2 trang 18 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính:
a) (a + b)(a + b);
b) (a – b)(a – b).
Lời giải:
a) \((a + b)(a + b) = a . a + a . b + b . a + b . b = a^2 + 2ab + b^2\);
b) \((a – b)(a – b) = a . a – a . b – b . a + b . b = a^2 – 2ab + b^2\).
Luyện tập 2 trang 19 Toán 8 Tập 1: Tính:
a) \((x + \dfrac{1}{2})^2\);
b) \((2x + y)^2\);
c) \((3 – x)^2\);
d) \((x – 4y)^2\).
Lời giải:
Luyện tập 3 trang 19 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng dạng bình phương của một tổng hoặc một hiệu:
a) \(y^2 + y + \dfrac{1}{4}\);
b) \(y^2 + 49 – 14y\).
Lời giải:
a) \(y^2 + y + \dfrac{1}{4} = y^2 + 2.\dfrac{1}{2}y + (\dfrac{1}{2})^2 = (y+\dfrac{1}{2})^2\)
b) \(y^2 + 49 – 14y = y^2 – 2 . 7 . y + 7^2 = (y – 7)^2\).
Luyện tập 4 trang 19 Toán 8 Tập 1: Tính nhanh: \(49^2\).
Lời giải:
Ta có \(49^2 = (50 – 1)^2 = 50^2 – 2 . 50 . 1 + 1^2\)
= 2500 – 100 + 1 = 2400 + 1 = 2401.
Hoạt động 3 trang 19 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính: (a – b)(a + b).
Lời giải:
Ta có: \((a – b)(a + b) = a . a + a . b – b . a + b . b = a^2 – b^2\).
Luyện tập 5 trang 20 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng tích:
a) \(9x^2 – 16\);
b) \(25 – 16y^2\).
Lời giải:
Giải thích:
a) \(9x^2 – 16 = (3x)^2 – 4^2 = (3x + 4)(3x – 4)\);
b) \(25 – 16y^2 = 5^2 – (4y)^2 = (5 + 4y)(5 – 4y)\).
Luyện tập 6 trang 20 Toán 8 Tập 1: Tính:
a) (a – 3b)(a + 3b);
b) (2x + 5)(2x – 5);
c) (4y – 1)(4y + 1).
Lời giải:
a) \((a – 3b)(a + 3b) = a^2 – (3b)^2 = a^2 – 9b^2\);
b) \((2x + 5)(2x – 5) = (2x)^2 – 5^2 = 4x^2 – 25\);
c) \((4y – 1)(4y + 1) = (4y)^2 – 1 = 16y^2 – 1\).
Luyện tập 7 trang 20 Toán 8 Tập 1: Tính nhanh: 48 . 52.
Lời giải:
Ta có: \(48 . 52 = (50 – 2)(50 + 2) = 50^2 – 2^2 = 2500 – 4 = 2496\).
Hoạt động 4 trang 20 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính:
a) \((a + b)(a + b)^2\);
b) \((a – b)(a – b)^2\).
Lời giải:
a) \((a + b)(a + b)^2 = (a + b)(a^2 + 2ab + b^2)\)
\(= a . a^2 + a . 2ab + a . b^2 + b . a^2 + b . 2ab + b . b^2\)
\(= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3\)
\(= a^3 + 3a^2b + 3ab^2 + b^3\).
b) \((a – b)(a – b)^2 = (a – b)(a^2 – 2ab + b^2)\)
\(= a . a^2 – a . 2ab + a . b^2 – b . a^2 + b . 2ab – b . b^2\)
\(= a^3 – 2a^2b + ab^2 – a^2b + 2ab^2 – b^3\)
\(= a^3 – 3a^2b + 3ab^2 – b^3\).
Luyện tập 8 trang 21 Toán 8 Tập 1: Tính:
a) \((3 + x)^3\);
b) \((a + 2b)^3\);
c) \((2x – y)^3\).
Lời giải:
a) \((3 + x)^3 = 3^3 + 3 . 3^2 . x + 3 . 3 . x^2 + x^3 = 27 + 27x + 9x^2 + x^3\);
b) \((a + 2b)^3 = a^3 + 3 . a^2 . 2b + 3 . a . (2b)^2 + (2b)^3\)
\(= a^3 + 6a^2b + 12ab^2 + 8b^3\);
c) \((2x – y)^3 = 2x^3 – 3 . (2x^)2 . y + 3 . 2x . y^2 – y^3\)
\(= 2x^3 – 12x^2y + 6xy^2 – y^3\).
Luyện tập 9 trang 21 Toán 8 Tập 1: Viết biểu thức sau dưới dạng lập phương của một hiệu: \(8x^3 – 36x^2y + 54xy^2 – 27y^3\).
Lời giải:
Ta có: \(8x^3 – 36x^2y + 54xy^2 – 27y^3\)
\(= (2x)^3 – 3 . (2x)^2 . 3y + 3 . 2x . (3y)^2 – (3y)^3\)
\(= (2x – 3y)^3\).
Luyện tập 10 trang 21 Toán 8 Tập 1: Tính nhanh: \(101^3 – 3 . 101^2 + 3 . 101 – 1\).
Lời giải:
Ta có \(101^3 – 3 . 101^2 + 3 . 101 – 1\)
\(= 101^3 – 3 . 101^2 . 1 + 3 . 101 . 12 – 13\)
\(= (101 – 1)^3 = 100^3 = 1 000 000\).
Hoạt động 5 trang 21 Toán 8 Tập 1: Với a, b là hai số thực bất kì, thực hiện phép tính:
a) \((a + b)(a^2 – ab + b^2)\);
b) \((a – b)(a^2 + ab + b^2)\).
Lời giải:
a) \((a + b)(a^2 – ab + b^2) = a . a^2 – a . ab + a . b^2 + b . a^2 – b . ab + b . b^2\)
\(= a^3 – a^2b + ab^2 + a^2b – ab^2 + b^3 = a^3 + b^3\)
.b) \((a – b)(a^2 + ab + b^2) = a . a^2 + a . ab + a . b^2 – b . a^2 – b . ab – b . b^2\)
= \(a^3 + a^2b + a^2b – a^2b – a^2b – b^3 = a^3 – b^3\).
Luyện tập 11 trang 22 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng tích:
a) \(27x^3 + 1\);
b) \(64 – 8y^3\).
Lời giải:
a) \(27x^3 + 1 = (3x)^3 + 13 = (3x + 1)[(3x)^2 – 3x . 1 + 12]\)
= \((3x + 1)(9x^2 – 3x + 1)\);
b) \(64 – 8y^3 = 43 – (2y)^3 = (4 + 2y)(4 – 2y)\).
Bài tập:
Bài 1 trang 23 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) \(4x^2 + 28x + 49\);
b) \(4a^2 + 20ab + 25b^2\);
c) \(16y^2 – 8y + 1\);
d) \(9x^2 – 6xy + y^2\).
Lời giải:
a) \(4x^2 + 28x + 49 = (2x)^2 + 2 . 2x . 7 + 72 = (2x + 7)^2\);
b) \(4a^2 + 20ab + 25b^2 = (2a)^2 + 2 . 2a . 5b + (5b)^2 = (2a + 5b)^2\);
c) \(16y^2 – 8y + 1 = (4y)^2 – 2 . 4y . 1 + 1^2 = (4y – 1)^2\);
d) \(9x^2 – 6xy + y^2 = (3x)^2 – 2 . 3x . y + y^2 = (3x – y)^2\).
Bài 2 trang 23 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
a) \(a^3 +12a^2 + 48a + 64\);
b) \(27x^3 + 54x^2y + 36xy^2 + 8y^3\);
c) \(x^3 – 9x^2 + 27x – 27\);
d) \(8a^3 – 12a^2b + 6ab^2 – b^3\).
Lời giải:
a) \(a^3 +12a^2 + 48a + 64 = a^3 + 3 . a^2 . 4 + 3 . a . 4^2 + 4^3 = (a + 4)^3\);
b) \(27x^3 + 54x^2y + 36xy^2 + 8y^3\)
= \((3x)^3 + 3 . (3x)^2 . 2y + 3 . 3x . (2y)^2 + (2y)^3\)
= \((3x + 2y)^3\);
c) \(x^3 – 9x^2 + 27x – 27 = x^3 – 3 . x^2 . 3 + 3 . x . 3^2 – 3^3 = (x – 3^)3\);
d) \(8a^3 – 12a^2b + 6ab^2 – b^3 = (2a)^3 – 3 . (2a)^2b + 3 . 2ab^2 – b^3 = (2a – b)^3\).
Bài 3 trang 23 Toán 8 Tập 1: Viết mỗi biểu thức sau dưới dạng tích:
a) \(25x^2 – 16\);
b) \(16a^2 – 9b^2\);
c) \(8x^3 + 1\);
d) \(125x^3 + 27y^3\);
e) \(8x^3 – 125\);
g) \(27x^3 – y^3\).
Lời giải:
a) \(25x^2 – 16 = (5x)^2 – 42 = (5x + 4)(5x – 4)\);
b) \(16a^2 – 9b^2 = (4a)^2 – (3b)^2 = (4a + 3b)(4a – 3b)\);
c) \(8x^3 + 1 = (2x)^3 + 1 = (2x + 1)[(2x)^2 + 2x . 1 + 1^2] = (2x + 1)(4x^2 + 2x + 1)\);
d) \(125x^3 + 27y^3 = (5x)^3 + (3y)^3 = (5x + 3y)[(5x)^2 + 5x . 3y + (3y)^2]\)
= \((5x + 3y)(25x^2 + 15xy + 9y^2)\);
e) \(8x^3 – 125 = (2x)^3 – 5^3 = (2x + 5)[(2x)^2 + 2x . 5 + 5^2]\)
= \((2x + 5)(4x^2 + 10x + 25)\);
g) \(27x^3 – y^3 = (3x)^3 – y^3 = (3x + y)(3x – y)\).
Bài 4 trang 23 Toán 8 Tập 1: Tính giá trị của mỗi biểu thức:
a) A = \(x^2 + 6x + 10\) tại x = −103;
b) B = \(x^3 + 6x^2 + 12x + 12\) tại x = 8.
Lời giải:
a) Ta có A = \(x^2 + 6x + 10 = x^2 + 6x + 9 + 1 = (x + 3)2 + 1\).
Thay x = −103 vào biểu thức A, ta được:
A = \((−103 + 3)^2 + 1 = (−100)^2 + 1 = 10 000 + 1 = 10 001\).
Vậy A = 10 001 tại x = −103.
b) Ta có B = \(x^3 + 6x^2 + 12x + 12 = x^3 + 3 . x^2 . 2 + 3 . x . 2^2 + 2^3 + 4\)
= \((x + 2)^3 + 4\).
Thay x = 8 vào biểu thức B, ta được:
B = \((8 + 2)^3 + 4 = 10^3 + 4\) = 1004.
Vậy B = 1004 tại x = 8.
Bài 5 trang 23 Toán 8 Tập 1: Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x:
a) C = \((3x – 1)^2 + (3x + 1)^2 – 2(3x – 1)(3x + 1)\);
b) D = \((x + 2)^3 – (x – 2)^3 – 12(x^2 + 1)\);
c) E = \((x + 3)(x^2 – 3x + 9) – (x – 2)(x^2 + 2x + 4)\);
d) G = \((2x – 1)(4x^2 + 2x + 1) – 8(x + 2)(x^2 – 2x + 4)\).
Lời giải:
a) Ta có C = \((3x – 1)^2 + (3x + 1)^2 – 2(3x – 1)(3x + 1)\)
= \([(3x – 1) – (3x + 1)]^2= (3x – 1 – 3x – 1)^2\)
= \((– 1 – 1)^2= (–2)^2= 4\).
Vậy biểu thức C không phụ thuộc vào biến x.
b) D = \((x + 2)^3 – (x – 2)^3 – 12(x^2 + 1)\)
= \([(x + 2) – (x – 2)][(x + 2)^2 + (x + 2)(x – 2) + (x – 2)^2] – 12(x^2 + 1)\)
= \((x + 2 – x + 2)[(x + 2)^2 + x^2 – 2^2 + (x – 2)^2] – 12x^2 – 12\)
= \(4(x^2 + 4x + 4 + x^2 – 4 +x^2– 4x + 4) – 12x^2 – 12\)
= \(4(3x^2 + 4) – 12x^2 – 12\)
= \(12x^2 + 16 – 12x^2 – 12 = 4\).
Vậy biểu thức D không phụ thuộc vào biến x.
c) E = \((x + 3)(x^2 – 3x + 9) – (x – 2)(x^2 + 2x + 4)\)
= \((x^3 + 3^3) – (x^3 – 2^3) = x^3 + 27 – x^3+ 8 = 35\).
Vậy biểu thức E không phụ thuộc vào biến x.
d) G = \((2x – 1)(4x^2 + 2x + 1) – 8(x + 2)(x^2 – 2x + 4)\)
= \([(2x)^3 – 13]– 8(x^3 + 23) = (8x^3 – 1) – 8(x^3 + 8)\)
= \(8x^3 – 1–8x^3 – 64 = – 65\).
Vậy biểu thức D không phụ thuộc vào biến x.
Bài 6 trang 23 Toán 8 Tập 1: Tính nhanh: \((0,76)^3 + (0,24)^3 + 3 . 0,76 . 024\).
Lời giải:
Ta có \((0,76)^3 + (0,24)^3 + 3 . 0,76 . 024\)
= \((0,76 + 0,24)^3 – 3 . 0,76 . 024 . (0,76 + 024) + 3 . 0,76 . 024\)
= \(13 – 3 . 0,76 . 024 . 1 + 3 . 0,76 . 024\)
= \(1 – 3 . 0,76 . 024 + 3 . 0,76 . 024 = 1\).
Vậy \((0,76)^3 + (0,24)^3 + 3 . 0,76 . 024 = 1\).
-//-
Hy vọng với nội dung trả lời chi tiết câu hỏi trong Bài 3: Hằng đẳng thức đáng nhớ giúp học sinh nắm được nội dung bài học và ghi nhớ những nội dung chính, quan trọng trong chương trình học Toán học 8.