Giải bài tập 70 trang 141 sgk Toán 7 tập 1 - Hình học

Câu hỏi

Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh rằng tam giác AMN là tam giác cân

b) Kẻ BH ⊥ AM, kẻ CK ⊥ AN. Chứng minh rằng BH = CK

c) CMR AH = AK

d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì ? Vì sao

e) Khi góc BAC = 60⁰ và BM = CN = BC hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC

Đáp Án

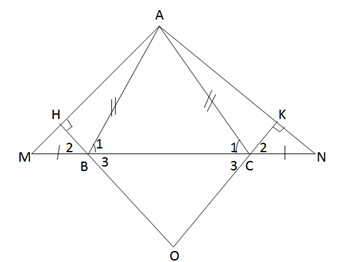
a) ∆ABC cân, suy ra góc B₁ = góc C₁ (1)

góc B₁ + góc ABM = 180⁰ (hai góc kề bù)  (2)

góc C₁ + góc ACN = 180⁰ (hai góc kề bù)  (3)

Từ (1), (2), (3) => góc AMB = góc ACN

Xét ∆ABM và ∆CAN có:

+) AB = AC (gt)

+) góc ABM = góc ACN (cmt)

+) BM = CN (gt)

=> ∆ABM = ∆CAN (c-g-c)

Suy ra góc M = góc N

Vậy ∆AMN là tam giác cân ở A.

b) Hai tam giác vuông ∆BHM và ∆CKN có :

BM = CN (gt)

góc M = góc N (CM từ a)

Nên ∆BHM  = ∆CHN (cạnh huyền, góc nhọn)

Suy ra BH = CK.

c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)

Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).

Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK

Vậy AH = AK.

d) ∆BHM = ∆CKN suy ra góc B₂ = góc C₂

Mà góc B₂ = góc B₃ (đối đỉnh); góc C₂ = góc C₃

Nên góc B₃ = C₃

Vậy ∆OBC là tam giác cân.

e)

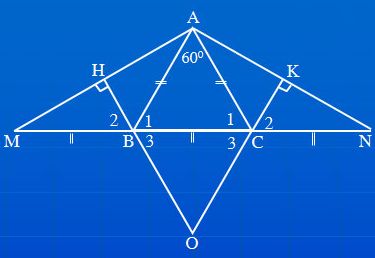
Tam giác cân ABC góc BAC = 60⁰ nên là tam giác đều hay AB = BC = AC

Mặt khác: BM = CN = BC (gt)

Do đó: AB = BC = AC = BM = CN

Ta có: góc ABM = góc ACN = 120⁰ (cùng bù với góc 60⁰)

Vì AB = BM (cmt) nên ∆ABM cân ở B suy ra góc M = góc BAM = (180⁰-120⁰)/2 = 30⁰

Suy ra góc ANM = góc AMN = 30⁰

Và góc MAN = 180⁰ - (AMN + ANM)
= 180⁰ - 2.30⁰ = 120⁰

Vậy ∆AMN có góc M = góc N = 30⁰; góc A = 120⁰

+ ∆BHM có góc M = 30⁰ nên góc B₂ = 60⁰ (hai góc phụ nhau)

Suy ra góc B₃ = 60⁰

Tương tự góc C₃ = 60⁰

Tam giác OBC có B₃ = C₃ = 60⁰ nên tam giác OBC là tam giác đều.

(Tam giác cân có một góc bằng 60⁰ nên là tam giác đều).