Câu hỏi:
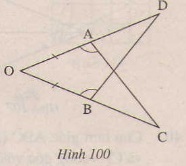
Trên hình 100 ta có OA=OB, OAC=OBD.
Chứng minh rằng AC=BD.
Đáp Án
Xét ∆OAC và ∆OBD, có:
góc OAC = góc OBD(gt)
OA = OB(gt)
góc O chung.
Nên ∆OAC = ∆OBD(g.c.g)
Suy ra: AC = BD
Giải bài tập 36 trang 123 sgk Toán 7 tập 1 - Hình học
Hướng dẫn giải và đáp án bài 36 trang 123 sách giáo khoa Toán lớp 7 tập 1, phần Hình học.
Mục lục nội dung
giai bai tap 36 trang 123 sgk toan 7 tap 1 hinh hoc
giai bai tap 36 trang 123 sgk toan 7 tap 1 hinh hoc