Bài 9 trang 119 SGK Toán 8 tập 1

Lời giải bài 9 trang 119 sgk Toán 8 tập 1 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 2 phần hình học để tự tin hoàn thành tốt các bài tập về diện tích hình chữ nhật khác.

Đề bài 9 trang 119 SGK Toán 8 tập 1

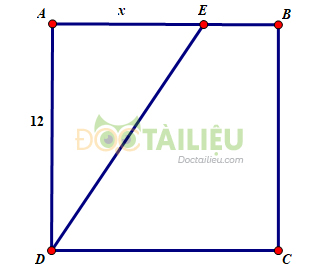
\(ABCD\) là một hình vuông cạnh \( 12cm\), \(AE = x(cm)\) (h.\(123\)). Tính \(x\) sao cho diện tích tam giác \(ABE\) bằng \(\dfrac{1}{3}\) diện tích hình vuông \(ABCD\).

» Bài tập trước: Bài 8 trang 118 sgk Toán 8 tập 1

Giải bài 9 trang 119 sgk Toán 8 tập 1

Hướng dẫn cách làm

Áp dụng:

• + Công thức tính diện tích tam giác vuông: Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông.
• + Công thức tính diện tích hình vuông: Diện tích hình vuông bằng bình phương cạnh của nó.

Bài giải chi tiết

Dưới đây là các cách giải bài 9 trang 119 SGK Toán 8 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

Diện tích tam giác vuông \(ABE\) là: \(S' = \dfrac{1}{2}AB.A{\rm{E}} = \dfrac{1}{2}.12.x = 6x\left( {c{m^2}} \right)\)

Diện tích hình vuông là: \(S = 12.12 = 144\left( {c{m^2}} \right)\)

Theo đề bài ta có: \(S' = \dfrac{S}{3}\)

hay \(6x = \dfrac{{144}}{3} = 48\left( {c{m^2}} \right)\)

\( \Rightarrow x = 48:6 = 8\left( {cm} \right)\)

Vậy \( AE = 8cm\).

» Bài tập tiếp theo: Bài 10 trang 119 sgk Toán 8 tập 1

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 9 trang 119 sgk toán 8 tập 1. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.