Bài 89 trang 111 SGK Toán 8 tập 1

Bạn tìm tài liệu hướng dẫn giải bài 89 trang 111 SGK Toán 8 tập 1? không cần tìm nữa...

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án... mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức Toán 8 chương 1 phần hình học Tứ giác đã được học trên lớp

Xem chi tiết!

Đề bài 89 trang 111 SGK Toán 8 tập 1

Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Gọi \(D\) là trung điểm của \(AB, E\) là điểm đối xứng với \(M\) qua \(D\).

a) Chứng minh rằng điểm \(E\) đối xứng với điểm \(M\) qua \(AB\).

b) Các tứ giác \(AEMC, AEBM\) là hình gì? Vì sao?

c) Cho \(BC = 4cm\), tính chu vi tứ giác \(AEBM\).

d) Tam giác vuông \(ABC\), có điều kiện gì thì \(AEBM\) là hình vuông?

» Bài tập trước: Bài 88 trang 111 sgk Toán 8 tập 1

Giải bài 89 trang 111 sgk Toán 8 tập 1

Hướng dẫn cách làm

- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành.

- Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

- Hình bình hành có hai đường chéo vuông góc là hình thoi

- Hình thoi có một góc vuông là hình vuông.

Bài giải chi tiết

Dưới đây là các cách giải bài 89 trang 111 SGK Toán 8 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

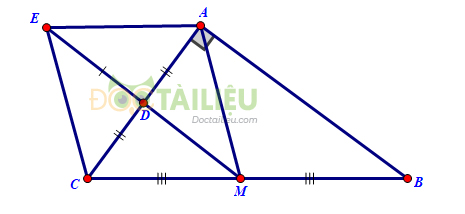
a) Ta có \(MB = MC\) (vì \(M\) là trung điểm của \(BC\) ),

\(BD = DA\) (vì \(D\) là trung điểm của \(AB\) )

nên \(MD\) là đường trung bình của \(∆ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)

Do đó \(MD // AC\) (tính chất đường trung bình của tam giác)

Do \(AC ⊥ AB\) (gt) nên \(MD ⊥ AB\)

Ta có \(AB\) là đường trung trực của \(ME\) (do \(AB ⊥ ME\) tại \(D\) và \(DE = DM\)) nên \(E\) đối xứng với \(M\) qua \(AB\).

b) Ta có: \(EM // AC\) (do \(MD // AC\))

\(EM = AC\) (cùng bằng \(2DM\))

Suy ra \(AEMC\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Tứ giác \(AEBM\) có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành.

Hình bình hành \(AEBM\) có \(AB ⊥ EM\) (chứng minh trên) nên \(AEBM\) là hình thoi (dấu hiệu nhận biết hình thoi)

c) Ta có \(BC = 4 cm \Rightarrow BM = 2 cm\) (do \(M\) là trung điểm \(BC\))

Chu vi hình thoi \(AEBM\) bằng \(4.BM = 4. 2 = 8(cm)\)

d) Hình thoi \(AEBM\) là hình vuông \(⇔ AB = EM ⇔ AB = AC\)

Vậy nếu \(ABC\) vuông có thêm điều kiện \(AB = AC\) (tức là tam giác \(ABC\) vuông cân tại \(A\)) thì \(AEBM\) là hình vuông.

\(⇔∆ABC\) cân tại \(A\) (dấu hiệu nhận biết tam giác cân)

Vậy nếu \(∆ABC\) vuông có thêm điều kiện cân tại \(A\) thì \(AEBM\) là hình vuông.

» Bài tập tiếp theo: Bài 90 trang 112 sgk Toán 8 tập 1

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 89 trang 111 sgk toán 8 tập 1. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.