Bài 7 trang 12 SGK Toán 9 tập 2

Bạn muốn giải bài 7 trang 12 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 chương 3 phần đại số để tự tin giải tốt các bài tập khác về hệ hai phương trình bậc nhất hai ẩn.

Đề bài 7 trang 12 SGK Toán 9 tập 2

Cho hai phương trình \(2x + y = 4\) và \(3x + 2y = 5\).

a) Tìm nghiệm tổng quát của mỗi phương trình trên.

b) Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong mỗi một hệ trục tọa độ, rồi xác định nghiệm chung của chúng.

» Bài tập trước: Bài 6 trang 11 SGK Toán 9 tập 2

Giải bài 7 trang 12 SGK Toán 9 tập 2

Hướng dẫn cách làm

a) Từ phương trình \(ax+by=c\)  \((\) với \(b \ne 0)\) rút biến \(y\) theo biến \(x\), ta được: \(y=-\dfrac{a}{b}x+\dfrac{c}{b}\). Khi đó nghiệm tổng quát của phương trình trên là:

\(\left\{ \matrix{x \in R \hfill \cr y =-\dfrac{a}{b}x+\dfrac{c}{b} \hfill \cr} \right.\)

b) +) Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đã cho trên cùng một hệ trục tọa độ.

+) Xác định giao điểm. Thử lại tọa độ vào hai phương trình, nếu thỏa mãn thì tọa độ đó là nghiệm chung của hệ hai phương trình.

Đáp án chi tiết

Dưới đây là các cách giải bài 7 trang 12 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

a) Ta có:

+) \(2x{\rm{ }} + {\rm{ }}y{\rm{ }} = {\rm{ }}4{\rm{ }} \Leftrightarrow {\rm{ }}y{\rm{ }} = {\rm{ }} - 2x{\rm{ }} + {\rm{ }}4{\rm{ }}\).

Do đó phương trình có nghiệm dạng tổng quát là:

\(\left\{ \matrix{x \in R \hfill \cr y = - 2{\rm{x}} + 4 \hfill \cr} \right.\)

+) \(3x + 2y = 5 \Leftrightarrow y =  - \dfrac{3}{2}x + \dfrac{5}{2}\).

Do đó phương trình có nghiệm tổng quát như sau:

\(\left\{ \matrix{ x \in R\hfill \cr y = - \dfrac{3}{2}x + \dfrac{5}{2} \hfill \cr} \right.\)

b) +) Vẽ \((d)\): \(y =-2x+ 4\)

Cho \(x = 0 \Rightarrow y = 4\)  được  \(A(0; 4)\).

Cho \(y = 0 \Rightarrow x = 2\)  được  \(B(2; 0)\).

Tập nghiệm của phương trình là đường thẳng \((d)\) đi qua hai điểm \(A,\ B\).

+) Vẽ \((d')\): \(y =-\dfrac{3}{2}x+\dfrac{ 5}{2}\)

Cho \(x = 0 \Rightarrow y = \dfrac{5 }{2}\),  ta được  \(M{\left(0;\dfrac{5}{2} \right)}\).

Cho \(y = 0 \Rightarrow x = \dfrac{5 }{3}\),  ta được  \(N {\left( \dfrac{5}{3};0 \right)}\).

Tập nghiệm của phương trình là đường thẳng \((d')\) đi qua hai điểm \(M,\ N\).

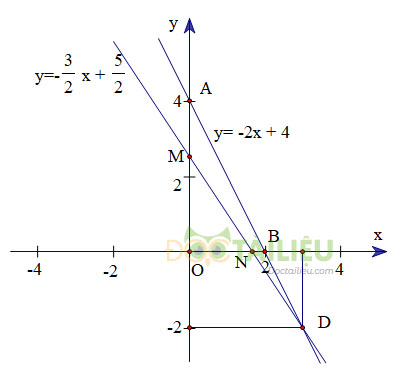
Hai đường thẳng cắt nhau tại \(D(3; -2)\).

Thay \(x = 3, y = -2\) vào từng phương trình ta được:

\(2 . 3 + (-2) = 4\) và \(3 . 3 + 2 . (-2) = 5\) (thỏa mãn)

Vậy \((3; -2)\) là nghiệm chung của các phương trình đã cho.

» Bài tiếp theo: Bài 8 trang 12 SGK Toán 9 tập 2

Nội dung trên đã giúp bạn nắm được cách làm bài 7 trang 12 SGK Toán 9 tập 2. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.