Đề bài
Cho tam giác ABC không vuông. Gọi H là trực tâm của nó.
a) Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ta trực tâm của tam giác đó.
b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác HAB, HAC.
Phương pháp
Sử dụng dữ kiện H là trực tâm tam giác ABC, tức H là giao điểm của ba đường cao của tam giác ABC.
Hướng dẫn giải
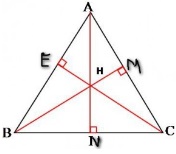
Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E.
a) ∆HBC có:
HN ⊥ BC nên HN là đường cao
BE ⊥ HC nên BE là đường cao
CM ⊥ BH nên CM là đường cao
Mà A là giao điểm của các đường thẳng HN, BE, CM.
Vậy A là trực tâm của ∆HBC
b) Chứng mình tương tự ta tìm được trực tâm của ∆AHB là C, trực tâm của ∆AHC là B.
giai bai 61 tr 83 sgk toan 7 t2
giai bai 61 tr 83 sgk toan 7 t2