Bài 56 trang 129 SGK Toán 8 tập 2

Lời giải bài 56 trang 129 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 4 phần hình học Hình lăng trụ đứng, hình chóp đều để tự tin hoàn thành tốt các bài tập hình lăng trụ đứng và hình chóp đều khác.

Đề bài 56 trang 129 SGK Toán 8 tập 2

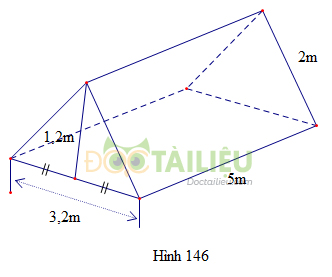
Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình 146).

a) Tính thể tích khoảng không ở bên trong lều.

b) Số vải bạt cần có để dựng lều đó là bao nhiêu?

(Không tính các mép và nếp gấp của lều).

» Bài tập trước: Bài 55 trang 128 SGK Toán 8 tập 2

Giải bài 56 trang 129 sgk Toán 8 tập 2

Hướng dẫn cách làm

Áp dụng công thức tính thể tích của hình lăng trụ đứng tam giác, công thhức tính diện tích xung quanh, diện tích toàn phần của hình lăng trụ.

Bài giải chi tiết

Dưới đây là các cách giải bài 56 trang 129 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

a) Lều là lăng trụ đứng tam giác.

Diện tích đáy (tam giác):

\(S = \dfrac{1}{2}.3,2.1,2 = 1,92\left( {{m^2}} \right)\)

Thể tích khoảng không bên trong lều là:

\(V = Sh = 1,92. 5 = 9,6 (m^3)\)

b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là \(5\,m\) và \(3,2\,m\).

Diện tích xung quanh lăng trụ là:

\({S_{xq}}= 2ph = (2 + 2+ 3,2) .5 = 36 (m^2)\)

Diện tích toàn phần:

\({S_{tp}} = {S_{xq}} + 2{S_đ}= 36 + 2.1,92 \)\(\,= 39,84 (m^2)\)

Diện tích mặt bên kích thước \(5\,m\) và \(3,2\,m\) là:

\(S = 5.3,2 = 16 (m^2)\)

Vậy số vải bạt cần có để dựng lều là:

\(39,84 - 16 = 23,84 (m^2)\)

Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.

» Bài tập tiếp theo: Bài 56 trang 129 SGK Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 56 trang 129 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.