Bài 5 trang 37 SGK Toán 9 tập 2

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án bài 5 trang 37 SGK Toán 9 tập 2 mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức chương 4 phần đại số Toán 9 đã được học trên lớp về đồ thị của hàm số y = ax2.

Đề bài 5 trang 37 SGK Toán 9 tập 2

Cho ba hàm số:

\(y = \dfrac{1}{2}{x^2};\ y = {x^2};\ y = 2{x^2}\).

a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm ba điểm \(A,\  B,\ C\) có cùng hoành độ \(x = -1,5\) theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.

c) Tìm ba điểm \(A',\  B',\  C'\) có cùng hoành độ \(x = 1,5\) theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của \(A\) và \(A'\), \(B\) và \(B'\), \(C\) và \(C'\).

d) Với mỗi hàm số trên, hãy tìm giá trị của \(x\) để hàm số đó có giá trị nhỏ nhất.

» Bài tập trước: Bài 4 trang 36 SGK Toán 9 tập 2

Giải bài 5 trang 37 SGK Toán 9 tập 2

Hướng dẫn cách làm

Đáp án chi tiết

Dưới đây là các cách giải bài 5 trang 37 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

a) +) Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\)

Cho \(x=1 \Rightarrow y=\dfrac{1}{2}\). Đồ thị đi qua \({\left(1; \dfrac{1}{2} \right)}\).

Cho \(x=-1 \Rightarrow y=\dfrac{1}{2}\). Đồ thị đi qua \({\left(-1; \dfrac{1}{2} \right)}\).

Cho \(x=2 \Rightarrow y=\dfrac{1}{2}. 2^2=2\). Đồ thị hàm số đi qua điểm \((2; 2)\).

Cho \(x=-2 \Rightarrow y=\dfrac{1}{2}.(-2)^2=2\). Đồ thị hàm số đi qua điểm \((-2; 2)\).

Đồ thị hàm số \(y=\dfrac{1}{2}x^2\) là parabol đi qua gốc tọa độ và các điểm trên.

+) Vẽ đồ thị hàm số \(y=x^2\).

Cho \(x=1 \Rightarrow y=1\). Đồ thị đi qua \((1; 1)\).

Cho \(x=-1 \Rightarrow y=(-1)^2\). Đồ thị đi qua \((-1; 1)\).

Cho \(x=2 \Rightarrow y=2^2=4\). Đồ thị hàm số đi qua điểm \((2; 4)\).

Cho \(x=-2 \Rightarrow y=(-2)^2=4\). Đồ thị hàm số đi qua điểm \((-2; 4)\).

Đồ thị hàm số \(y=x^2\) là parabol đi qua gốc tọa độ và các điểm trên.

+) Vẽ đồ thị hàm số \(y=2x^2\).

Cho \(x=1 \Rightarrow y=2.1^2=2\). Đồ thị đi qua \((1; 2)\).

Cho \(x=-1 \Rightarrow y=2.(-1)^2\). Đồ thị đi qua \((-1; 2)\).

Cho \(x=2 \Rightarrow y=2.2^2=8\). Đồ thị hàm số đi qua điểm \((2; 8)\).

Cho \(x=-2 \Rightarrow y=2.(-2)^2=8\). Đồ thị hàm số đi qua điểm \((-2; 8)\).

Đồ thị hàm số \(y=2x^2\) là parabol đi qua gốc tọa độ và các điểm trên.

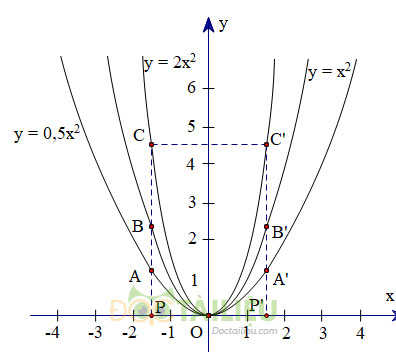
b)

Xác định điểm P trên trục Ox có hoành độ \(x =  - 1,5\). Qua P kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị \(y = \dfrac{1}{2}{x^2};y = {x^2};y = 2{x^2}\) lần lượt tại \(A;B;C\)

Gọi \({y_A},{y_B},{y_C}\) lần lượt là tung độ các điểm \(A,\ B,\ C\). Ta có:

\(\eqalign{ & {y_A} = {1 \over 2}{( - 1,5)^2} = {1 \over 2}.2,25 = 1,125 \cr & {y_B} = {( - 1,5)^2} = 2,25 \cr & {y_C} = 2{( - 1.5)^2} = 2.2,25 = 4,5 \cr} \)

c) Xác định điểm \(P'\)  trên trục Ox có hoành độ \(x = 1,5\). Qua \(P'\)  kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị \(y = \dfrac{1}{2}{x^2};y = {x^2};y = 2{x^2}\) lần lượt tại \(A';B';C'\)

Gọi \({y_{A'}},{y_{B'}},{y_{C'}}\)  lần lượt là tung độ các điểm \(A', B', C'\) . Ta có:

\(\eqalign{ & {y_{A'}} = {1 \over 2}{(1,5)^2} = {1 \over 2}.2,25 = 1,125 \cr & {y_{B'}} = {(1,5)^2} = 2,25 \cr & {y_{C'}} = 2{(1.5)^2} = 2.2,25 = 4,5 \cr} \)

Kiểm tra tính đối xứng: \(A\) và \(A'\), \(B\) và \(B'\), \(C\) và \(C'\) đối xứng với nhau qua trục tung \(Oy\).

d) Với mỗi hàm số đã cho ta đều có hệ số \(a > 0\) nên O là điểm thấp nhất của đồ thị.

Vậy với  \(x = 0\) thì các hàm số trên đều có giả trị nhỏ nhất \(y=0.\)

» Bài tiếp theo: Bài 6 trang 38 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 5 trang 37 Toán đại số 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.