Bài 46 trang 124 SGK Toán 8 tập 2

Lời giải bài 46 trang 124 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 chương 4 phần hình học để tự tin hoàn thành tốt các bài tập thể tích của hình chóp đều khác.

Đề bài 46 trang 124 SGK Toán 8 tập 2

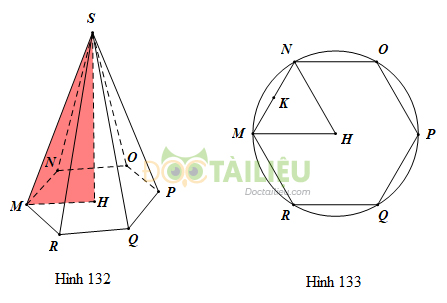
\(S.MNOPQR\) là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm \(H\), đi qua sáu đỉnh của đáy) \(HM = 12cm\)(h.133), chiều cao \(SH = 35cm\). Hãy tính:

a) Diện tích đáy và thể tích của hình chóp (biết \(\sqrt{108}\approx 10,39\));

b) Độ dài cạnh bên \(SM\) và diện tích toàn phần của hình chóp (biết \(\sqrt{1333}\approx 36,51\) ).

» Bài tập trước: Bài 45 trang 124 SGK Toán 8 tập 2

Giải bài 46 trang 124 sgk Toán 8 tập 2

Hướng dẫn cách làm

Tính thể tích hình chóp theo công thức:   \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

Bài giải chi tiết

Dưới đây là các cách giải bài 46 trang 124 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

a) Tam giác \(HMN \) là tam giác đều.

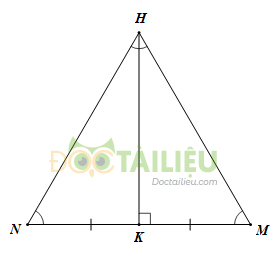
Đường cao của tam giác là:

\(HK = \sqrt{HM^{2}- KM^{2}}\) \( = \sqrt{HM^{2}- {\left( {\dfrac{{MN}}{2}} \right)^2}} \)

\(= \sqrt{12^{2}- 6^{2}} = \sqrt{108}\approx  10,39(cm) \)

Diện tích đáy của hình chóp lục giác đều chính là \(6\) lần diện tích của tam giác đều \(HMN\).

Diện tích đáy của hình chóp là:

\(S_{đ} =6.\dfrac{1}{2}. MN. HK = 6.\dfrac{1}{2}. 12. 10,39 \) \(=374,04(cm^2) \)

Thể tích của hình chóp:

\(V =\dfrac{1}{3}. S_{đ}. SH = \dfrac{1}{3}. 374,04 . 35 \) \(= 4363,8(cm^3) \)

b) Trong tam giác vuông \(SMH\) có:

\(SM= \sqrt{SH^{2}+ MH^{2}} = \sqrt{35^{2}+ 12^{2}}\) \(=\sqrt{1369} = 37 (cm)\)

Đường cao của mỗi mặt bên là :

\(h = SK =\sqrt{SM^{2}- KM^{2}} \)

= \(\sqrt{37^{2}- 6^{2}} = \sqrt{1333}\approx 36,51 (cm) \)

Diện tích xung quanh hình chóp là :

\( S_{xq} =  p.d = \dfrac{1}{2}.6. MN. SK \)

\( =\dfrac{1}{2}. 6.12.36,51 = 1314,36 (cm^2)\)

Diện tích toàn phần của hình chóp là:

\(S_{tp} = S_{xq} +S_{đ} = 1314,36 + 374,04 \) \(= 1688,4 (cm^2) \)

» Bài tập tiếp theo: Bài 47 trang 124 SGK Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 46 trang 124 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.