Bài 40 trang 83 SGK Toán 9 tập 2

Đáp án bài 40 trang 83 SGK Toán 9 tập 2 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 chương 3 phần hình học về góc có đỉnh bên trong đường tròn, góc ở đỉnh bên ngoài đường tròn.

Đề bài 40 trang 83 SGK Toán 9 tập 2

Qua điểm $S$ nằm bên ngoài đường tròn $(O)$, vẽ tiếp tuyến $SA$ và cát tuyến $SBC$ của đường tròn. Tia phân giác của $\widehat{BAC}$ cắt dây $BC$ tại $D.$ Chứng minh $SA = SD.$

» Bài tập trước: Bài 39 trang 83 SGK Toán 9 tập 2

Giải bài 40 trang 83 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

+) Số đo của góc tạo bởi tiếp tuyến của dây cung bằng nửa số đo cung bị chắn.

Đáp án chi tiết

Dưới đây là các cách giải bài 40 trang 83 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

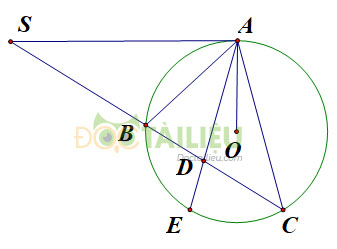
Gọi $E$ là giao điểm thứ hai của $AD$ với đường tròn $(O).$

Xét đường tròn $(O)$ ta có:

+) $\widehat{ADS}$ là góc có đỉnh nằm trong đường tròn chắn cung $AB$ và $CE.$

$\Rightarrow \widehat {ADS}=\dfrac{sđ\overparen{AB}+sđ\overparen{CE}}{2}.$  (1)

+) $\widehat{SAD}$ là góc tạo bởi tia tiếp tuyến và dây cung chắn cung $AE.$

$\Rightarrow \widehat {SAD}=\dfrac{1}{2} sđ\overparen{AE}.$  (2)

+) Có: $\widehat {BAE} = \widehat {EAC}$ (do $AE$ là phân giác góc $BAC$

$\Rightarrow$ $\overparen{BE}=\overparen{EC}$ (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).

$\Rightarrow sđ\overparen{AB} + sđ\overparen{EC}$$= sđ\overparen{AB} + sđ\overparen{BE}=sđ\overparen{AE}$ (3)

Từ (1), (2), (3) $\Rightarrow\widehat {ADS}=\widehat {SAD}$$\Rightarrow$ tam giác $SDA$ cân tại $S$ hay $SA=SD$.

» Bài tiếp theo: Bài 41 trang 83 SGK Toán 9 tập 2

Trên đây là nội dung hướng dẫn trả lời bài 40 trang 83 SGK Toán 9 tập 2 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.