Bài 40 trang 27 SGK Toán 9 tập 2

Để giải bài 40 trang 27 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết về cách làm bài, Đọc Tài Liệu sẽ giúp các bạn đưa ra đáp án chính xác nhất và ôn tập các kiến thức trong chương trình học Toán 9 chương 3: Hệ hai phương trình bậc nhất hai ẩn.

Đề bài 40 trang 27 SGK Toán 9 tập 2

Giải các hệ phương trình sau và minh họa hình học kết quả tìm được:

a)\(\left\{ \matrix{2{\rm{x}} + 5y = 2 \hfill \cr {\displaystyle{2 \over 5}}x + y = 1 \hfill \cr} \right.\)

b) \(\left\{ \matrix{0,2{\rm{x}} + 0,1y = 0,3 \hfill \cr 3{\rm{x}} + y = 5 \hfill \cr} \right.\)

c) \(\left\{ \matrix{{\displaystyle{3 \over 2}}x - y = {\displaystyle{1 \over 2}} \hfill \cr 3{\rm{x}} - 2y = 1 \hfill \cr} \right.\)

» Bài tập trước: Bài 39 trang 25 SGK Toán 9 tập 2

Giải bài 40 trang 27 SGK Toán 9 tập 2

Hướng dẫn cách làm

Đáp án chi tiết

Dưới đây là các cách giải bài 40 trang 27 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

\(\left\{ \matrix{ 2{\rm{x}} + 5y = 2 \hfill \cr {\displaystyle{2 \over 5}}x + y = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 2{\rm{x}} + 5y = 2 \hfill \cr - 2{\rm{x}} - 5y = - 5 \hfill \cr} \right.\)

Cộng vế với vế của hai phương trình trong hệ trên, ta được: \(2x + 5y +(-2x-5y)= 2-5 \)

\( \Leftrightarrow 0 =  - 3\)  (vô lý)

Vậy hệ đã cho vô nghiệm.

Minh họa hình học kết quả tìm được:

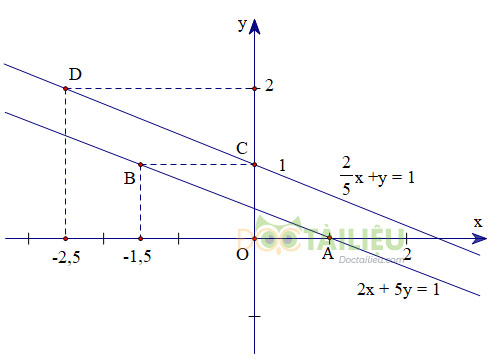
- Vẽ đồ thị hàm số \(2x + 5y = 2\).

Cho \(y = 0 ⇒  x = 1\). Ta xác định được điểm \(A(1; 0)\)

Cho \(y = 1 ⇒ x = -1,5\). Ta xác định được điểm \(B(-1,5; 1)\).

Đồ thị hàm số \(2x + 5y = 2\) là đường thẳng đi qua hai điểm A và B

-Vẽ đồ thị hàm số  \({\displaystyle{2 \over 5}}x + y = 1 \Leftrightarrow 2{\rm{x}} + 5y = 5\)

Cho \(x = 0 ⇒ y = 1\). Ta xác định được điểm \(C(0; 1)\)

Cho \(y = 2 ⇒ x = -2,5\). Ta xác định được điểm \(D(-2,5; 2)\)

Đồ thị hàm số \({\displaystyle{2 \over 5}}x + y = 1\) là đường thẳng đi qua hai điểm C và D.

Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm.

b) Giải hệ phương trình:

\(\left\{ \matrix{ 0,2{\rm{x}} + 0,1y = 0,3 \hfill \cr 3{\rm{x}} + y = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ - 2{\rm{x}} - y = - 3 \hfill \cr 3{\rm{x}} + y = 5 \, (2) \hfill \cr} \right.\)

Cộng vế với  vế của hai phương trình trên, ta được \(-2x-y+3x+y=-3+5\) \( \Leftrightarrow x = 2\)

Thế \(x = 2\) vào phương trình (2), ta được: \(6 + y = 5 ⇔ y = -1\)

Vậy nghiệm của hệ phương trình là \((x;y)=(2;-1)\)

Minh họa hình học:

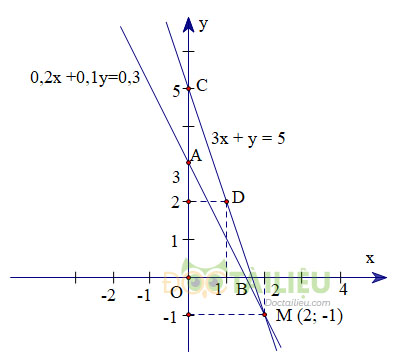
- Đồ thị hàm số \(0,2x + 0,1y = 0,3\) là một đường thẳng đi qua hai điểm:

\(A( 0; 3)\) và \(B(1,5; 0)\)

- Đồ thị hàm số \(3x + y = 5\) là một đường thẳng đi qua hai điểm \(C( 0;  5)\) và \(D( 1; 2)\)

- Đồ thị hai hàm số trên cắt nhau tại điểm: \(M( 2;  -1)\).

Vậy \((2; -1)\) là một nghiệm của hệ phương trình.

c) Giải hệ phương trình:

\(\left\{ \matrix{ {\displaystyle{3 \over 2}}x - y = {\displaystyle{1 \over 2}} \hfill \cr 3{\rm{x}} - 2y = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ - 3{\rm{x}} + 2y = - 1 \hfill \cr 3{\rm{x}} - 2y = 1 \hfill \cr} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}3x - 2y = 1\\ - 3x + 2y + 3x - 2y =  - 1 + 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}2y = 3x - 1\\0 = 0\left( {luôn \, đúng} \right)\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{3}{2}x - \dfrac{1}{2}\\x \in \mathbb{R}\end{array} \right.\)

Vậy hệ phương trình đã cho có vô số nghiệm.

Nghiệm tổng quát là \(\left( {x;{\displaystyle{3 \over 2}}x - {\displaystyle{1 \over 2}}} \right)\)  với \(x ∈ R\)

Minh họa hình học

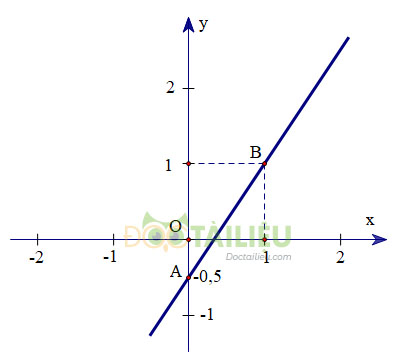
- Đồ thị hàm số \(\dfrac{3}{2}x - y = \dfrac{1}{2}\)  và đồ thị hàm số \(3x - 2y = 1\) cùng là một đường thẳng đi qua hai điểm \(A(0;  - {\displaystyle{1 \over 2}})\) và \(B(1;1)\) nên hai đường thẳng này trùng nhau. Vậy hệ phương trinh có vô số nghiệm.

» Bài tiếp theo: Bài 41 trang 27 SGK Toán 9 tập 2

Nội dung trên đã giúp bạn nắm được cách làm bài 40 trang 27 SGK Toán 9 tập 2. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.