Bài tập 4 trang 91 sgk Toán 7 tập 2

Đề bài

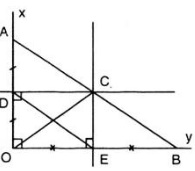
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường thẳng trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng:

a) CE = OD;                             b) CE ⊥ CD;

c) CA = CB;                             d) CA // DE;

e) Ba điểm A, B, C thẳng hàng.

Phương pháp

- Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.

- Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.

- Áp dụng tiên đề Ơ-clit: Qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

- Áp dụng định lí: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.

Hướng dẫn giải bài 4 trang 91 sgk Toán 7

a) Ta có: Ox ⊥ Oy và CE ⊥ Oy ⇒ EC // Ox   (1)

Oy ⊥ Ox và CD ⊥Ox ⇒ DC // Oy   (2)

Từ (1) và (2) ta có: CE // Ox và DC // Oy ⇒ CE = OD (tính chất đoạn chắn)

b) Ta có CE // Ox (do (1)). Mà CD ⊥ Ox

Suy ra CD ⊥ CE (đpcm).

c) Vì C nằm trên đường trung trực của OA nên CA = CO  (3)

Vì C nằm trên đường trung trực của OB nên CB = CO  (4)

Từ (3) và (4) suy ra CA = CB (đpcm).

d) Xét hai tam giác vuông DAC và CED ta có:

CD: cạnh chung

Góc ADC = góc DEC = 90⁰

AD = CE (do OD = DA = CE)

Vậy ∆DAC = ∆CED (c.g.c)

=> góc ACD = góc EDC

Hơn nữa góc ACD so le trong với góc EDC

Suy ra CA // DE (đpcm).

e) Chứng minh tương tự như câu d suy ra CB // DE. Do đó theo tiên đề Ơ-clit ta suy ra hai đường thẳng BC và CA trùng nhau hay A, B, C thẳng hàng.

» Tham khảo thêm: Bài 5 trang 91 sgk Toán 7