Bài 37 trang 82 SGK Toán 9 tập 2

Bạn muốn giải bài 37 trang 82 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 chương 3 phần hình học để tự tin giải tốt các bài tập khác về góc có đỉnh bên trong đường tròn, góc ở đỉnh bên ngoài đường tròn.

Đề bài 37 trang 82 SGK Toán 9 tập 2

Cho đường tròn \((O)\) và hai dây \(AB\), \(AC\) bằng nhau. Trên cung nhỏ \(AC\) lấy một điểm \(M\). Gọi \(S\) là giao điểm của \(AM\) và \(BC\). Chứng minh: \(\widehat {ASC} = \widehat {MCA}.\)

» Bài tập trước: Bài 36 trang 82 SGK Toán 9 tập 2

Giải bài 37 trang 82 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.

Đáp án chi tiết

Dưới đây là các cách giải bài 37 trang 82 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

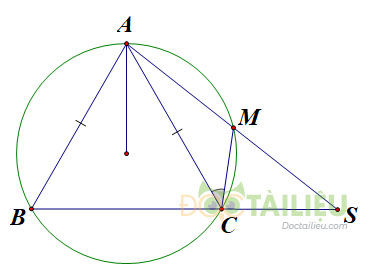
Xét đường tròn \((O)\), ta có:

\(\widehat{ASC}\) là góc có đỉnh ở ngoài đường tròn chắn cung \(MC\) và \(AB.\)

\(\Rightarrow \widehat{ASC} = \dfrac{sđ \overparen{AB}- sđ \overparen{MC}}{2}\) (1)

và \(\widehat {MCA}\) = \(\dfrac{sđ\overparen{AM}}{2}\)   (2) (góc nội tiếp chắn cung \(\overparen{AM}\))

Theo giả thiết thì: \(AB = AC => \overparen{AB}=\overparen{AC}\)  (hai dây bằng nhau căng hai cung bằng nhau).

\(\Rightarrow sđ\overparen{AB}-sđ\overparen{MC}=sđ\overparen{AC}-sđ\overparen{MC}=sđ\overparen{AM}\)  (3)

Từ (1), (2), (3) suy ra: \(\widehat {ASC}=\widehat {MCA}.\) (đpcm)

» Bài tiếp theo: Bài 38 trang 82 SGK Toán 9 tập 2

Nội dung trên đã giúp bạn nắm được cách làm bài 37 trang 82 SGK Toán 9 tập 2. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.