Bài 36 trang 82 SGK Toán 9 tập 2

Đáp án bài 36 trang 82 SGK Toán 9 tập 2 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 chương 3 phần hình học về góc có đỉnh bên trong đường tròn, góc ở đỉnh bên ngoài đường tròn.

Đề bài 36 trang 82 SGK Toán 9 tập 2

Cho đường tròn \((O)\) và hai dây \(AB\), \(AC\). Gọi \(M, N\) lần lượt là điểm chính giữa của cung \(AB\) và cung \(AC\). Đường thẳng \(MN\) cắt dây \(AB\) tại \(E\) và cắt dây \(AC\) tại \(H\). Chứng minh rằng tam giác \(AEH\) là tam giác cân.

» Bài tập trước: Bài 35 trang 80 SGK Toán 9 tập 2

Giải bài 36 trang 82 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Sử dụng: "Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn."

Đáp án chi tiết

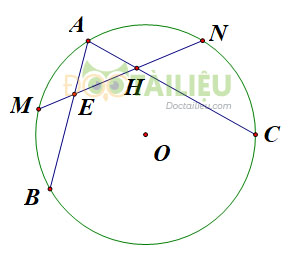
Ta có: \(\widehat {AHM}\)= \(\dfrac{sđ\overparen{AM}+sđ\overparen{NC}}{2}\,\,\, (1)\)

\(\widehat {AEN}\)= \(\dfrac{sđ\overparen{MB}+sđ\overparen{AN}}{2}\,\,\,  (2)\)

(Vì  \(\widehat {AHM}\) là góc có đỉnh cố định ở bên trong đường tròn chắn các cung \(AM\) và cung \(NC\), và  \(\widehat {AEN}\) là góc có đỉnh bên trong đường tròn chắn các cung \(AN\) và cung \( MB\)).

Theo gỉả thiết thì:

\(\overparen{AM}=\overparen{MB}   (3)\) (\(M\)

\(\overparen{NC}=\overparen{AN}    (4)\)  \(N\) là điểm chính giữa cung \(AC\)).

Từ (1),(2), (3), (4), suy ra \(\widehat {AHM}= \widehat {AEN}\) do đó \(∆AEH\) là tam giác cân (định nghĩa tam giác cân).

» Bài tiếp theo: Bài 37 trang 82 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 36 trang 82 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.