Giải bài tập 30 trang 67 sách giáo khoa Toán 7 tập 2 - Hình học

Đề bài

Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’.

a) So sánh các cạnh của tam giác BGG’ với các đường trung tuyến của tam giác ABC.

b) So sánh các đường trung tuyến của tam giác BGG’ với các cạnh của tam giác ABC.

Phương pháp

Áp dụng tính chất đường trung tuyến của tam giác.

Hướng dẫn giải

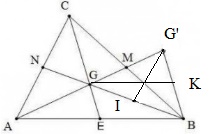
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC.

Gọi M, N, E lần lượt là trung điểm của BC, CA, AB.

- G là trọng tâm của ∆ABC

⇒ GA = 2/3 AM

Mà GA = GG’ (G là trung điểm của AG’)

⇒ GG' = 2/3 AM

- Vì G là trọng tâm của ∆ABC ⇒ GB = 2/3 BN

- Ta có:

GM = 1/2 AG AG (do G là trọng tâm) và AG = GG' (gt)

⇒ GM = 1/2 GG'

Xét ∆GMC và ∆G’MB có:

GM = MG'

MB = MC

Góc GMC = góc G'MB  (hai góc đối đỉnh)

Vậy  ∆GMC=∆G’MB.

⇒ BG' = CG

Mà CG = 2/3 CE (G là trọng tâm tam giác ABC)

⇒ BG' = 2/3 CE

Vậy mỗi cạnh của ∆BGG’ bằng 2/3 đường trung tuyến của ∆ABC.

b) So sánh các đường trung tuyến của ∆BGG’ với các cạnh của ∆ABC.

- Ta có: BM là đường trung tuyến ∆BGG’

Mà M là trung điểm của BC nên BM = 1/2 BC

Vì IG = 1/2 BG (Do I là trung điểm BG)

GN = 1/2 BF (G là trọng tâm)

⇒  IG = GN

Xét  ∆IGG’ và ∆NGA có:

IG = GN (cmt)

GG' = GA (gt)

góc IGG' = góc NGA (hai góc đối đỉnh)

Vậy ∆IGG’ = ∆NGA (c.g.c) ⇒  IG' = AN ⇒  IG' = AC/2

- Gọi K là trung điểm BG ⇒  GK là trung tuyến của ∆BGG’

Vì GE = 1/2 GC (G là trọng tâm tam giác ABC)

BG' = GC (cmt)

⇒  GE = 1/2 BG'

Mà K là trung điểm BG’ 
⇒
KG’ = EG

Vì ∆GMC = ∆G’MB (cmt)

⇒ góc GCM = góc G'BM (hai góc tương ứng)

⇒  CE // BG’ ⇒ góc AGE = góc AG'B (đồng vị)

Xét ∆AGE và ∆GG’K có:

EG = KG’ (cmt)

AG = GG' (gt)

góc AGE = góc AG'B (cmt)

Vậy ∆AGE = ∆GG’K (c.g.c) ⇒  AE = GK

Mà AE = 1/2 AB ⇒ GK = 1/2 AB

Vậy mỗi đường trung tuyến của ∆BGG’ bằng một nửa cạnh của tam giác ABC song song với nó.