Bài 3 trang 134 SGK Toán 9 tập 2

Để giải bài 3 trang 134 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết về cách làm bài, Đọc Tài Liệu sẽ giúp các bạn đưa ra đáp án chính xác nhất và ôn tập các kiến thức trong chương trình học Toán 9 ôn tập cuối năm phần hình học.

Đề bài 3 trang 134 SGK Toán 9 tập 2

Cho tam giác \(ABC\) vuông ở \(C\) có đường trung tuyến \(BN\) vuông góc với đường trung tuyến \(CM,\) cạnh \(BC = a.\) Tính độ dài đường trung tuyến \(BN.\)

» Bài tập trước: Bài 2 trang 134 SGK Toán 9 tập 2

Giải bài 3 trang 134 SGK Toán 9 tập 2

Hướng dẫn cách làm

Áp dụng công thức hệ thức lượng trong tam giác vuông và định lý Pi-ta-go.

Đáp án chi tiết

Dưới đây là các cách giải bài 3 trang 134 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

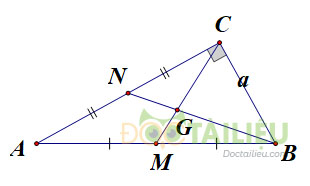
Gọi \(G\) là trọng tâm của tam giác \(ABC,\) ta có: \(\displaystyle BG = {2 \over 3}BN.\)

Áp dụng hệ thức lượng trong tam giác vuông \(CNB\) có đường cao \(CG\) ta có:

\(\eqalign{ & B{C^2} = BN.BG = BN.{2 \over 3}BN = {2 \over 3}B{N^2} \cr & \Rightarrow B{N^2} = {3 \over 2}B{C^2} = {{3{a^2}} \over 2} \cr & \Rightarrow BN = \sqrt {{{3{{\rm{a}}^2}} \over 2}} = {{a\sqrt 3 } \over {\sqrt 2 }} = {{a\sqrt 6 } \over 2}. \cr}\)

Vậy \(\displaystyle BN = {{a\sqrt 6 } \over 2}.\)

» Bài tiếp theo: Bài 4 trang 134 SGK Toán 9 tập 2

Trên đây là nội dung hướng dẫn trả lời bài 3 trang 134 SGK Toán 9 tập 2 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.