Bài 23 trang 123 SGK Toán 8 tập 1

Bạn muốn giải bài 23 trang 123 SGK Toán 8 tập 1? Đừng bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 8 chương 2 phần hình học để tự tin giải tốt các bài tập về diện tích tam giác khác

Đề bài 23 trang 123 SGK Toán 8 tập 1

Cho tam giác \(ABC\). Hãy chỉ ra một số vị trí của điểm \(M\) nằm trong tam giác đó sao cho:

\({S_{AMB}} + {S_{BMC}} = {S_{MAC}}\)

» Bài tập trước: Bài 22 trang 122 sgk Toán 8 tập 1

Giải bài 23 trang 123 sgk Toán 8 tập 1

Hướng dẫn cách làm

- Kẻ đường cao \(BH, MK.\)

- Áp dụng công thức tính diện tích tam giác: Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

Bài giải chi tiết

Dưới đây là các cách giải bài 23 trang 123 SGK Toán 8 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

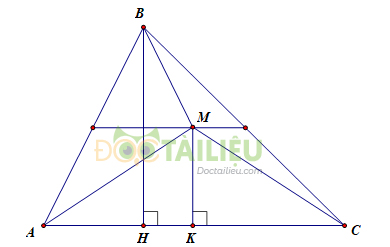
Kẻ đường cao \(BH, MK.\)

Theo giả thiết, \(M\) là điểm nằm trong tam giác \(ABC\) sao cho:

\({S_{AMB}} + {\rm{ }}{S_{BMC}} = {\rm{ }}{S_{MAC}}\)  (1)

Ta lại có: \({S_{AMB}} + {S_{BMC}} + {S_{MAC}} = {S_{ABC}}\)    (2)

Thay (1) vào (2) ta được: \({S_{MAC}}+ {S_{MAC}}={S_{ABC}}\)

Hay \({S_{MAC}} = \dfrac{1}{2}{S_{ABC}}\)

\(\Rightarrow \dfrac{1}{2}MK.AC = \dfrac{1}{2}\left( {\dfrac{1}{2}BH.AC} \right)\)

\(⇒MK = \dfrac{1}{2}BH\)

Do đó, \(M\) nằm trên đường thẳng sao cho khoảng cách từ \(M\) đến \(AC\) bằng \(\dfrac{1}{2}\) đường cao \(BH\).

Vậy điểm \(M\) nằm trong tam giác \(ABC\) và nằm trên đường trung bình ứng với cạnh \(AC\) của \(ΔABC\)

» Bài tập tiếp theo: Bài 24 trang 123 sgk Toán 8 tập 1

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 23 trang 123 sgk toán 8 tập 1. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.