Bài 21 trang 118 SGK Toán 9 tập 2

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án bài 21 trang 118 SGK Toán 9 tập 2 mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức chương 4 phần hình học Toán 9 đã được học trên lớp về Hình nón và Hình nón cụt.

Đề bài 21 trang 118 SGK Toán 9 tập 2

Cái mũ của chú hề với các kích thước cho theo hình vẽ(h97). Hãy tính tổng diện tích vải vẩn có để làm nên cái mũ (Không kể riềm, mép, phần thừa).

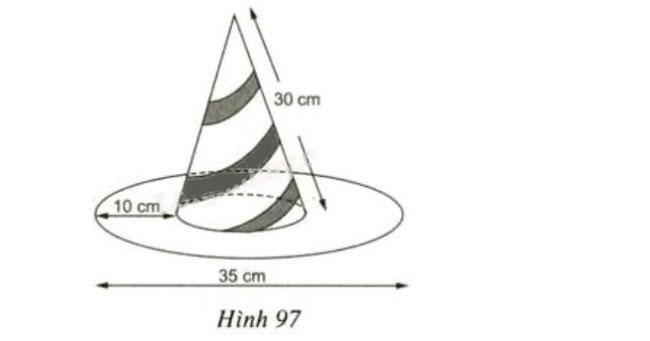
» Bài tập trước: Bài 20 trang 118 SGK Toán 9 tập 2

Giải bài 21 trang 118 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Diện tích phần vải cần để làm mũ = Diện tích vành mũ + Diện tích của phần trên mũ

= Diện tích hình vành khăn + Diện tích xung quanh hình nón.

+) Diện tích xung quanh của hình nón bán kính rr và đường sinh ll là: S_xq = πrl.

Đáp án chi tiết

Dưới đây là các cách giải bài 21 trang 118 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

Gọi \(S\) là diện tích vải cần có, \({S_{xq}}\) là diện tích xung quanh hình nón, \({S_{vk}}\) là diện tích hình vành khăn thì \(S = {S_{xq}} + {S_{vk}}\)

+ Đường kính đường tròn lớn là \(35cm\) nên bán kính đường tròn lớn là \(R = \dfrac{{35}}{2} = 17,5cm\)

Suy ra bán kính đường tròn nhỏ là \(r = 17,5 - 10 = 7,5cm\).

Với \(\pi  = 3,14\) ta có

+ Diện tích hình vành khăn là \({S_{vk}} = \pi {R^2} - \pi {r^2} = \pi .17,{5^2} - \pi .7,{5^2} = 785c{m^2}\,\)

+ Hình nón có đường sinh \(l = 30cm\) và bán kính đáy \(r = 7,5cm\) nên có diện tích xung quanh là \({S_{xq}} = \pi rl = \pi .7,5.30 = 706,5c{m^2}\)

Vậy diện tích vải cần làm mũ là \(S = {S_{vk}} + {S_{xq}} = 785 + 706,5 = 1491,5c{m^2}\) .

» Bài tiếp theo: Bài 22 trang 118 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 21 trang 118 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.