Bài 20 trang 118 SGK Toán 9 tập 2

Để giải bài 20 trang 118 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết về cách làm bài, Đọc Tài Liệu sẽ giúp các bạn đưa ra đáp án chính xác nhất và ôn tập các kiến thức trong chương trình học Toán 9 chương 4 phần hình học về Hình nón và Hình nón cụt.

Đề bài 20 trang 118 SGK Toán 9 tập 2

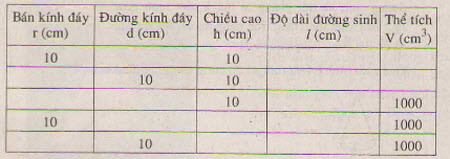
Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96)

» Bài tập trước: Bài 19 trang 118 SGK Toán 9 tập 2

Giải bài 20 trang 118 SGK Toán 9 tập 2

Hướng dẫn cách làm

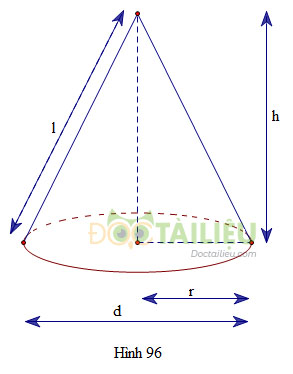
Cho hình nón có chiều cao \(h,\) bán kính đáy \(r\) và đường sinh \(l.\) Khi đó:

+) Đường kính đáy: \(d=2r.\)

+) Thể tích hình nón: \(V=\dfrac{1}{3} \pi r^2h.\)

+) Mối quan hệ \(l^2=h^2+r^2.\)

Đáp án chi tiết

Dưới đây là các cách giải bài 20 trang 118 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

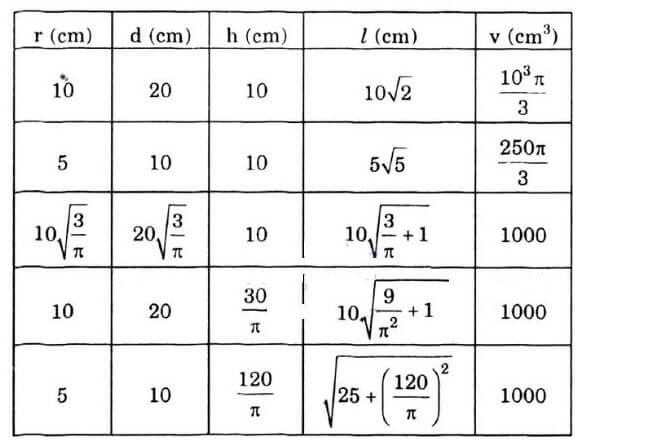
+ Dòng thứ nhất:

\(d = 2r = 1.10 = 20(cm)\)

\(l\) = \(\sqrt{h^2 + r^2 }= \sqrt{10^2 + 10^2}= 10\sqrt{2}\) (cm)

\(V\) = \(\dfrac{1}{3}\pi r^2h = \dfrac{1}{3}. 10^2. 10. \pi= 10^3. \pi.\dfrac{1}3\)  (\(cm^3\))

+ Dòng thứ hai: \(r\)= \(\dfrac{d}{2}= 5 (cm)\)

\(l\) = \(\sqrt{h^2 + r^2}= \sqrt{10^2 + 5^2}= 5\sqrt{5}\) (cm)

\(V\) =  \(\frac{1}{3}\pi r^2h = \dfrac{1}{3}. 5^2. 10. \pi= 250. \pi.\dfrac{1}3\) (cm³)

+ Dòng thứ ba:

Ta có \(V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow {r^2} = \dfrac{{3V}}{{\pi h}} = \dfrac{{3.1000}}{{\pi .10}} = \dfrac{{300}}{\pi }\, \Rightarrow r = 10\sqrt {\dfrac{3}{\pi }} \,cm\)

- Đường kính đáy \(d = 2r = 20\sqrt {\dfrac{3}{\pi }} \,cm\)

- Đường sinh \(l = \sqrt {{h^2} + {r^2}}  = \sqrt {100 + \dfrac{{300}}{\pi }}  = 10\sqrt {\dfrac{3}{\pi } + 1}  \)

+ Dòng thứ tư : Khi \(r = 10cm;V = 1000\,c{m^3}\)

Ta có \(V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.10}^2}}} = \dfrac{{30}}{\pi }cm\)

- Đường kính đáy \(d = 2r = 20cm\)

- Đường sinh \(l = \sqrt {{h^2} + {r^2}}  = \sqrt {\dfrac{{900}}{\pi } + 100}  = 10\sqrt {\dfrac{9}{{{\pi ^2}}} + 1} \)

+ Dòng thứ 5: Khi \(d = 10cm;V = 1000c{m^3}\) ta có \(r = \dfrac{d}{2} = 5cm\)

- Lại có \(V = \dfrac{1}{3}\pi {r^2}h \Leftrightarrow h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.5}^2}}} = \dfrac{{120}}{\pi }cm\)

- Đường sinh \(l = \sqrt {{r^2} + {h^2}}  = \sqrt {{5^2} + {{\left( {\dfrac{{120}}{\pi }} \right)}^2}}  \)

» Bài tiếp theo: Bài 21 trang 118 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 20 trang 118 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.