Đáp án bài 2 trang 71 sách giáo khoa hình học lớp 11

1. Đề bài

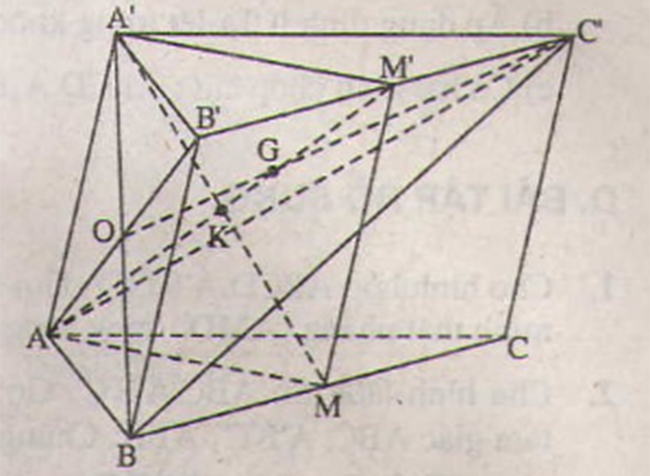
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.

• a) Chứng minh rằng AM song song với A’M’.
• b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.
• c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).
• d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.

2. Đáp án - hướng dẫn giải bài 2 trang 71

a) ABC . A′B′C′ là hình lăng trụ tam giác nên ta có: AA′ // MM′ và AA′ = MM′ nên suy ra AA′M′M là hình bình hành.

Do đó: AM // A′M′

b) Trong mp(AA′M′M) , gọi K = MA′ ∩ AM′ , K = A′M ∩ (AB′C′)

c) Trong (ABB′A′) gọi O = AB′ ∩ A′B Do đó: (AB′C′) ∩ (BA′C′) = d ≡ C′O

d) Trong (AB′C′) : gọi G = C′O ∩ AM′ , G ∈ AM′ ⊂ (AMM′) nên G = d ∩ (AMM′) .

Mà O, M′ lần lượt là trung điểm AB′ và B′C′ nên G là trọng tâm của tam giác AB′C′ .