Giải bài 2 trang 125 sách giáo khoa hình học lớp 11

1. Đề bài

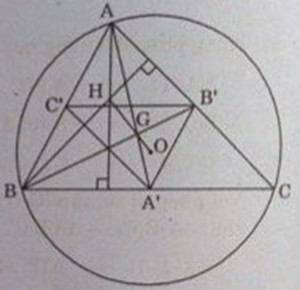
Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi G và H tương ứng là trọng tâm và trực tâm của tam giác, các điểm A', B',C' lần lượt là trung điểm của các cạnh BC, CA, AB.

(a) Tìm phép vị tự F biến A, B, C tương tứng thành A', B',C'

(b) Chứng minh rằng O, G, H thẳng hàng.

(c) Tìm ảnh của O qua phép vị tự F

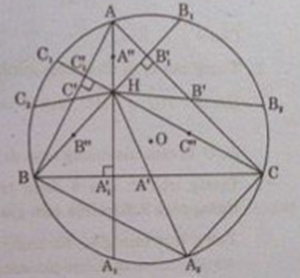
(d) Gọi A'', B'',C'' lần lượt là trung điểm của các đoạn thẳng AH, BH, CH; A1, B1,C1 theo thứ tự là giao điểm thứ hai của các tia AH, BH, CH với đường tròn (O); A'1, B'1,C'1 tương ứng là chân các đường cao đi qua A, B, C. Tìm ảnh của A, B, C,A1, B1,C1 qua phép vị tự tâm H tỉ số 1/2.

(e) Chứng minh chín điểm A', B',C',A'', B'',C'',A'1, B'1,C'1 cùng thuộc một đường tròn (đường tròn này gọi là đường tròn Ơ-le của tam giác ABC)

2. Đáp án - hướng dẫn giải bài 2 trang 125