Bài 16 trang 117 SGK Toán 9 tập 2

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án bài 16 trang 117 SGK Toán 9 tập 2 mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức chương 4 phần hình học Toán 9 đã được học trên lớp.

Đề bài 16 trang 117 SGK Toán 9 tập 2

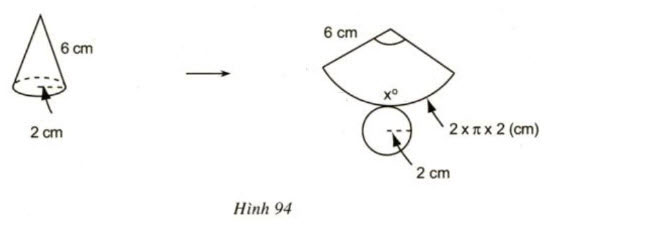
Cắt mặt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành 1 hình quạt. Biết bán kính của quạt  bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.

Quan sát hình 94 và tính số đo cung của hình quạt.

» Bài tập trước: Bài 15 trang 117 SGK Toán 9 tập 2

Giải bài 16 trang 117 SGK Toán 9 tập 2

Hướng dẫn cách làm

+ Sử dụng công thức tính chu vi đường tròn bán kính \(r\) là \(C = 2\pi r.\)

+ Sử dụng công thức tính độ dài cung tròn bán kính \(R\) và số đo cung \(n^\circ \) là \(l = \dfrac{{\pi Rn}}{{180}}\)

Đáp án chi tiết

Dưới đây là các cách giải bài 16 trang 117 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

+ Ta thấy hình nón có bán kính đáy \(r = 2cm\). Suy ra chu vi đáy \(C = 2\pi r = 2\pi .2 = 4\pi \left( {cm} \right)\)

+ Lại thấy hình quạt có bán kính \(R = 6cm\) và độ dài cung là \(l = C = 4\pi \left( {cm} \right)\)

Gọi \(x^\circ \,\left( {x > 0} \right)\) là số đo cung của hình quạt.

Khi đó độ dài cung là \(l = \dfrac{{\pi Rx}}{{180}} \Leftrightarrow \dfrac{{\pi .6.x}}{{180}} = 4\pi  \Leftrightarrow 6x = 720 \Leftrightarrow x = 120.\)  (tm)

Vậy số đo cung của hình quạt tròn là \(120^\circ .\)

» Bài tiếp theo: Bài 17 trang 117 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 16 trang 117 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.