Bài 13 trang 135 SGK Toán 9 tập 2

Bạn muốn giải bài 13 trang 135 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 để tự tin giải tốt các bài tập khác ôn tập cuối năm phần hình học.

Đề bài 13 trang 135 SGK Toán 9 tập 2

Cho đường tròn \((O)\), cung \(BC\) có số đo bằng \(120^0\), điểm \(A\) di chuyển trên cung lớn \(BC\). Trên tia đối tia \(AB\) lấy điểm \(D\) sao cho \(AD = AC\). Hỏi điểm \(D\) di chuyển trên đường nào?

» Bài tập trước: Bài 12 trang 135 SGK Toán 9 tập 2

Giải bài 13 trang 135 SGK Toán 9 tập 2

Hướng dẫn cách làm

+ Tính \(\widehat {BDC}\) dựa vào tính chất góc nội tiếp rồi sử dụng quỹ tích cung chứa góc dựng trên đoạn \(BC.\)

+ Xác định giới hạn quỹ tích của điểm \(D\) rồi kết luận.

Đáp án chi tiết

Dưới đây là các cách giải bài 13 trang 135 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

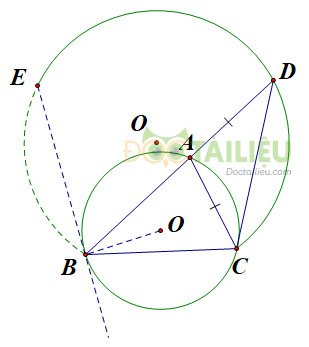
Ta có  \(\displaystyle \widehat A = {1 \over 2}sđ\overparen{BC}\)\(= {60^0}\);\( \displaystyle \widehat {B{\rm{D}}C} = {1 \over 2}{.60^0} = {30^0}.\) (số đo góc nội tiếp bằng nửa số đo cung bị chắn.)

Như vậy, điểm \(D\) tạo với hai mút của đoạn thẳng \(BC\) cố định một góc \(\widehat {B{\rm{D}}C} = {30^0}\) nên \(D\) chuyển động trên cung chứa góc \(30^0\) dựng trên \(BC.\)

Ta có, khi \(A ≡ B\) thì \(D ≡ E\) và khi \(A ≡ C\) thì \(D ≡ C.\)

Vậy khi \(A\) di chuyển trên cung lớn \(BC\) thì \(D\) di chuyển trên cung \(CE\) thuộc cung chứa góc \(30^0\) dựng trên \(BC.\)

» Bài tiếp theo: Bài 14 trang 135 SGK Toán 9 tập 2

Nội dung trên đã giúp bạn nắm được cách làm bài 13 trang 135 SGK Toán 9 tập 2. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.