Đáp án bài 12 trang 101 sách giáo khoa hình học 12

Đề bài

Trong không gian O x y z cho bốn điểm A ( 3 ; − 2 ; − 2 ) , B ( 3 ; 2 ; 0 ) , C ( 0 ; 2 ; 1 ) và D ( − 1 ; 1 ; 2 )

a) Viết phương trình mặt phẳng ( B C D ) . Suy ra A B C D là một tứ diện.

b) Viết phương trình mặt cầu ( S ) tâm A và tiếp xúc với mặt phẳng ( B C D ) .

c) Tìm toạ độ tiếp điểm của ( S ) và mặt phẳng ( B C D ) .

Hướng dẫn giải

a) Mặt phẳng (BCD) đi qua B và nhận 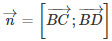 là 1 VTPT.

- Chứng minh điểm A không thuộc mặt phẳng (BCD), từ đó suy ra ABCD là tứ diện.

b) Mặt cầu tâm A , tiếp xúc với mp ( B C D ) có bán kính bằng khoảng cách từ A đến mp ( B C D ) Sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng.

c) H là hình chiếu của điểm A trên mặt phẳng (BCD).

- Viết phương trình đường thẳng d đi qua A và vuông góc với mặt phẳng BCD.

- Tìm giao điểm của đường thẳng d và mặt phẳng (BCD). Khi đó giao điểm trên chính là điểm H cần tìm.

Đáp án bài 12 trang 101 sgk hình học lớp 12