Bài 11 trang 135 SGK Toán 9 tập 2

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án bài 11 trang 135 SGK Toán 9 tập 2 mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức ôn tập cuối năm phần hình học Toán 9.

Đề bài 11 trang 135 SGK Toán 9 tập 2

Từ một điểm \(P\) ở ngoài đường tròn \((O)\), kẻ cát tuyến \(PAB\) và \(PCD\) tới đường tròn. Gọi \(Q\) là một điểm nằm trên cung nhỏ \(BD\) (không chứa \(A\) và \(C\)) sao cho \(sđ\overparen{BQ}=42^0\) và \(sđ\overparen{QD}=38^0\). Tính tổng \(\widehat {BP{\rm{D}}} + \widehat {AQC}.\)

» Bài tập trước: Bài 10 trang 135 SGK Toán 9 tập 2

Giải bài 11 trang 135 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.

+) Số đo góc nội tiếp bằng nửa số đo cung bị chắn.

Đáp án chi tiết

Dưới đây là các cách giải bài 11 trang 135 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

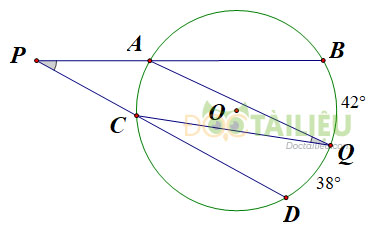
Ta có \(\widehat {BP{\rm{D}}}\) là góc ở ngoài đường tròn (O) nên:

\(\displaystyle \widehat {BPD} = {sđ\overparen{BQD} -sđ\overparen{AC}\over 2}\) (góc có đỉnh nẳm ngoài đường tròn chắn cung \(AC\) và \(BD\)).

Ta có \(\widehat {AQC}\) là góc nội tiếp trong đường tròn (O) nên:

\(\displaystyle \widehat {AQC} = {1 \over 2}sđ\overparen{AC}\)  (góc nội tiếp chắn cung \(AC\)).

\(\displaystyle \Rightarrow \widehat {BPD} + \widehat {AQC} = {sđ\overparen{BQD} -sđ\overparen{AC} \over 2} + {1 \over 2}sđ\overparen{AC}\)

\(\displaystyle ={1 \over 2}sđ\overparen{BQD}={{{{42}^0} + {{38}^0}} \over 2} = {40^0}.\)

Vậy \(\widehat {BP{\rm{D}}} + \widehat {AQC} = {40^0}.\)

» Bài tiếp theo: Bài 12 trang 135 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 11 trang 135 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.