Hướng dẫn giải bài 10 trang 54 SGK hình học lớp 11

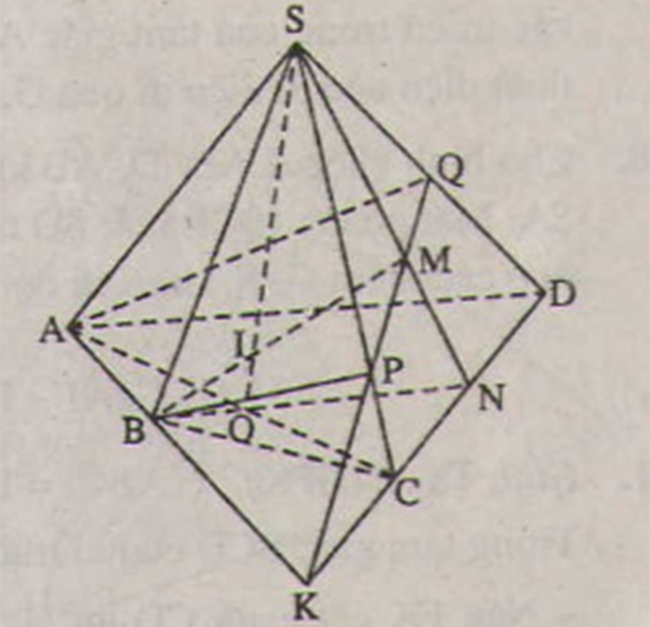
1. Đề bài

Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.

• a) Tìm giao điểm N của đường thẳng CD và mp(SBM).
• b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).
• c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC).
• d) Tìm giao điểm P của SC và mặt phẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).

2. Đáp án - hướng dẫn giải bài 10 trang 54

a) Trong (SCD ) kéo dài SM cắt CD tại N . Do đó: N = CD ∩ (SBM)

b) (SBM) ≡ (SBN) . Trong (ABCD) gọi O = AC ∩ BN Do đó: SO = (SAC) ∩ (SBM) .

c) Trong (SBN) gọi I là giao của MB và SO . Do đó: I = BM ∩ (SAC)

d) Trong (ABCD) , gọi giao điểm của AB và CD là K . Trong (SCD ) , gọi P = MK ∩ SC Do đó: P = SC ∩ (ABM) Trong (SDC) gọi Q = MK ∩ SD Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM ) là KQ .