Bài 10 trang 39 SGK Toán 9 tập 2

Đáp án bài 10 trang 39 SGK Toán 9 tập 2 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 chương 4 phần đại số về đồ thị của hàm số y = ax2.

Đề bài 10 trang 39 SGK Toán 9 tập 2

Cho hàm số \(y =  - 0.75{x^2}\). Qua đồ thị của hàm số đó, hãy cho biết khi \(x\) tăng từ \(-2\) đến \(4\) thì giá trị nhỏ nhất và giá trị lớn nhất của \(y\) là bao nhiêu ?

» Bài tập trước: Bài 9 trang 39 SGK Toán 9 tập 2

Giải bài 10 trang 39 SGK Toán 9 tập 2

Hướng dẫn cách làm

Đáp án chi tiết

Dưới đây là các cách giải bài 10 trang 39 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

Ta có bảng giá trị hàm số \(y =  - 0.75{x^2}\)

Vẽ parabol đi qua gốc tọa độ và các điểm có tọa độ \(\left( { - 4; - 12} \right);\left( { - 2; - 3} \right);\left( {2; - 3} \right);\left( {4; - 12} \right)\) ta được đồ thị hàm số \(y =  - 0,75{x^2}\)

Vẽ đồ thị: \(y =  - 0.75{x^2}\)

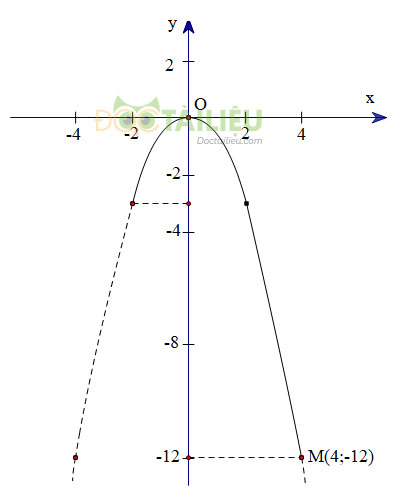
Đồ thị hàm số \(y=-0,75x^2\) với \(x\) từ \(-2\) đến \(4\) là đường cong nét liền trên hình vẽ.

Ta thấy: Điểm thấp nhất của phần đồ thị nét liền trên hình là điểm \(M(4;-12\) và điểm cao nhất là gốc tọa độ \(O(0;0)\).

Vậy giá trị lớn nhất của hàm số là \(0\). Giá trị thấp nhất của hàm số là \(-12\).

» Bài tiếp theo: Bài 11 trang 42 SGK Toán 9 tập 2

Trên đây là nội dung hướng dẫn trả lời bài 10 trang 39 SGK Toán 9 tập 2 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.