Bài 1 trang 134 SGK Toán 9 tập 2

Đáp án bài 1 trang 134 SGK Toán 9 tập 2 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 ôn tập cuối năm phần hình học.

Đề bài 1 trang 134 SGK Toán 9 tập 2

Chu vi hình chữ nhật \(ABCD\) là \(20cm\). Hãy tìm giá trị nhỏ nhất của độ dài đường chéo \(AC\).

» Bài tập trước: Bài 18 trang 133 SGK Toán 9 tập 2

Giải bài 1 trang 134 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Áp dụng định lý Pi-ta-go.

+) Đánh giá \(A^2+m \ge m\), dấu "=" xảy ra khi \(A=0.\)

Đáp án chi tiết

Dưới đây là các cách giải bài 1 trang 134 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

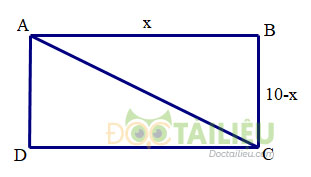
Gọi \(x\) (\(cm\)) là độ dài cạnh \(AB\)

Vì  nửa chu vi hình chữ nhật đã cho là: \(20:2=10 \, cm\) nên \(AB+BC=10cm\) suy ra  \(BC=10 – x \, (cm).\)

Áp dụng định lí Py-ta-go trong tam giác vuông \(ABC\), ta có:

\(\eqalign{ & A{C^2} = A{B^2} + B{C^2} \cr & = {x^2} + {\left( {10 - x} \right)^2} \cr & = 2\left( {{x^2} - 10{\rm{x}} + 50} \right) \cr & = 2\left[ {{{\left( {x - 5} \right)}^2} + 25} \right] \cr}\)

Vì \((x-5)^2 \geq 0 \Rightarrow A{C^2} = 2{\left( {x - 5} \right)^2} + 50 \ge 50 \)

Đẳng thức xảy ra khi : \(x – 5 = 0 ⇔ x = 5\)

Vậy giá trị nhỏ nhất của đường chéo AC là \(\sqrt50 = 5\sqrt2\) (\(cm\))

» Bài tiếp theo: Bài 2 trang 134 SGK Toán 9 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 1 trang 134 SGK Toán 9 tập 2. Mong rằng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.