Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2020 Chuyên Phổ thông năng khiếu và đáp án được Đọc Tài Liệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.
NEW: Đề thi chuyên Toán Phổ thông Năng khiếu năm 2021
Đề thi vào lớp 10 năm 2020
Chi tiết đề thi vào lớp môn Toán của trường Phổ thông năng khiếu như sau:
Đại học Quốc gia TP.HCM ĐỀ CHÍNH THỨC | KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC: 2020 - 2021 Môn: Toán |

Đáp án




Câu 3 ảnh:
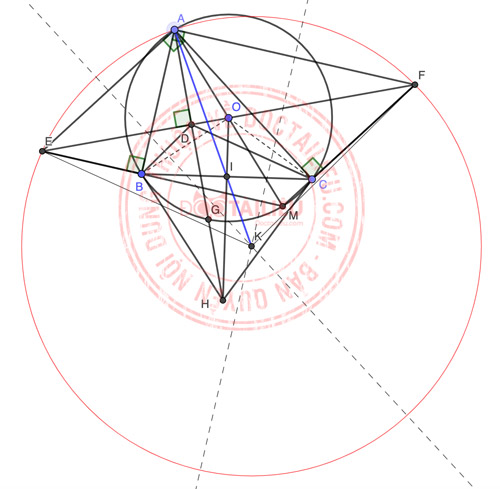
d)
Gọi J là điểm đối xứng của A qua K, dễ thấy AJ là đường kính của đường tròn (AEF).
Gọi AK cắt BC tại I.
Xét △ADE và △AFJ ta có:
∠ADE = ∠AFJ = 90°
∠AED = ∠AEF = ∠AJF (góc nt cùng chắn cung AF)
Suy ra △ADE ∽ △AFJ ⇒ ∠EAD = ∠JAF = ∠KAF
hay ∠EAB + ∠BAD = ∠KAC + ∠CAF ⇒ ∠BAD = ∠KAC (vì ∠EAB = ∠CAF cmt)
Xét △ABG và △AIC ta có:
∠BAG = ∠BAD = ∠KAC = ∠IAC (cmt)
∠BGA = ∠BCA = ∠ICA (góc nt cùng chắn cung AF)
Suy ra △ABG ∽ △AIC ⇒ \(\dfrac{BG}{IC} = \dfrac{AB}{AI} \)
Tương tự ta có △ACG ∽ △AIB ⇒ \(\dfrac{CG}{IB} = \dfrac{AC}{AI} \)
Chia vế theo vế cho 2 biểu thức trên, ta có:
\(\dfrac{BG}{IC}:\dfrac{CG}{IB} = \dfrac{AB}{AI} :\dfrac{AC}{AI}\)
\(\Leftrightarrow \dfrac{IB}{IC}= \dfrac{AB}{AC} .\dfrac{CG}{BG} = 1\) (cm phần c)
⇒ I là trung điểm BC, hay AK luôn đi qua trung điểm của BC là điểm cố định (đpcm).

Bài 5:
ĐKXĐ: xy; yz; zx > 0
a)
Xét hai trường hợp:
*) Trường hợp 1: x, y, z cùng dương.
Không mất tính tổng quát, giả sử x = max{x;y;z}
⇒ \(\dfrac{x}{\sqrt{yz}} + \sqrt{\dfrac{x}y} + \sqrt{\dfrac{x}z} \geq 3 > 1 = k\)
Mâu thuẫn.
*) Trường hợp 2: x, y, z cùng âm. Đặt a = -x; b = -y; z = -c (a; b; c > 0)
Khi đó phương trình có thể viết thành:
\(\left\{ \matrix{ -\dfrac{a}{\sqrt{bc}} + \sqrt{\dfrac{a}b} + \sqrt{\dfrac{a}c} = 1 \hfill \cr -\dfrac{b}{\sqrt{ca}} + \sqrt{\dfrac{b}c} + \sqrt{\dfrac{b}a} = 1 \hfill \cr -\dfrac{c}{\sqrt{ab}} + \sqrt{\dfrac{c}a} + \sqrt{\dfrac{c}b} = 1 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ -a + \sqrt{ac} + \sqrt{ab} = \sqrt{bc} \hfill \cr -b + \sqrt{ba} + \sqrt{bc} = \sqrt{ca} \hfill \cr -a + \sqrt{cb} + \sqrt{ca} = \sqrt{ab} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ a - \sqrt{ac} - \sqrt{ab} + \sqrt{bc} =0 \hfill \cr b - \sqrt{ba} - \sqrt{bc} + \sqrt{ca} =0 \hfill \cr a - \sqrt{cb} - \sqrt{ca} + \sqrt{ab} =0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ (\sqrt{a} - \sqrt{b})(\sqrt{a} - \sqrt{c}) =0 \hfill \cr (\sqrt{b} - \sqrt{a})(\sqrt{b} - \sqrt{c})=0 \hfill \cr (\sqrt{c} - \sqrt{b})(\sqrt{c} - \sqrt{a})=0 \hfill \cr} \right.\)
\(\Leftrightarrow a=b=c\)
KL: với k = 1 thì hệ đã cho có nghiệm (-t; -t; -t) với t ∈ ℝ*.
b)
Giả sử tồn tại số thực k ≥ 2 và k ≠ 3 sao cho hệ đã cho có nghiệm \((x_0;y_0;z_0)\).
Xét hai trường hợp sau:
*) Trường hợp 1: \((x_0;y_0;z_0)\) cùng dương. Ta có:
\(\left\{ \matrix{ (\sqrt{x_0} + \sqrt{y_0})(\sqrt{x_0} + \sqrt{z_0}) =(k+1)\sqrt{y_0z_0} \hfill \cr (\sqrt{y_0} + \sqrt{z_0})(\sqrt{y_0} + \sqrt{x_0}) =(k+1)\sqrt{z_0x_0} \hfill \cr (\sqrt{z_0} + \sqrt{x_0})(\sqrt{z_0} + \sqrt{y_0}) =(k+1)\sqrt{x_0y_0} \hfill \cr} \right.\)
⇒ \(\sqrt{y_0z_0} (\sqrt{y_0} + \sqrt{z_0}) =\sqrt{z_0x_0} (\sqrt{z_0} + \sqrt{x_0}) = \sqrt{x_0y_0} (\sqrt{x_0} + \sqrt{y_0}) \) (1)
Không mất tính tổng quát, giả sử:
\(x_0\geq y_0\geq z_0\). Ta có:
\(\sqrt{z_0x_0} (\sqrt{z_0} + \sqrt{x_0}) \leq \sqrt{x_0y_0} (\sqrt{x_0} + \sqrt{y_0}) \)
Kết hợp với (1) thì dấu bằng phải xảy ra, tức là
\(x_0 = z_0\), mà \(x_0\geq y_0\geq z_0\) ⇒ \(x_0 = y_0 = z_0\).
Thay lại vào hệ, ta có k = 3, mâu thuẫn.
*) Trường hợp 2: \((x_0;y_0;z_0)\) cùng âm.
Đặt \(a = -x_0; \space b = -y_0; \space z = -c_0\) (a; b; c > 0)
Ta có:
\(\left\{ \matrix{ -\dfrac{a}{\sqrt{bc}} + \sqrt{\dfrac{a}b} + \sqrt{\dfrac{a}c} = k \hfill \cr -\dfrac{b}{\sqrt{ca}} + \sqrt{\dfrac{b}c} + \sqrt{\dfrac{b}a} = k \hfill \cr -\dfrac{c}{\sqrt{ab}} + \sqrt{\dfrac{c}a} + \sqrt{\dfrac{c}b} = k \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ (\sqrt{a} - \sqrt{b})(\sqrt{a} - \sqrt{c}) =(1-k)\sqrt{bc} \hfill \cr (\sqrt{b} - \sqrt{a})(\sqrt{b} - \sqrt{c})=(1-k)\sqrt{ca} \hfill \cr (\sqrt{c} - \sqrt{b})(\sqrt{c} - \sqrt{a})=(1-k)\sqrt{ab} \hfill \cr} \right.\)
Không mất tính tổng quát, giả sử:
\(a \geq b \geq c \). Ta có:
\((1-k)\sqrt{bc} = (\sqrt{a} - \sqrt{b})(\sqrt{a} - \sqrt{c}) \geq 0\)
\(\Leftrightarrow k \leq 1\) mâu thuẫn.
Vậy điều giả sử là sai, suy ra hệ vô nghiệm với \(k \geq2 ; k ≠3\).
Xem thêm:
- Đáp án đề thi vào lớp 10 môn Văn không chuyên năm 2020 PTNK
- Đáp án đề thi vào lớp 10 môn Toán không chuyên năm 2020 PTNK
Có thể các em quan tâm:
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 năm 2020 của trường THPT Năng khiếu được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
