Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm 2020 - đề khảo sát chất lượng đối với các em học sinh lớp 9 vừa ra em nhé:
Đề thi
Câu 1: (2,0 điểm)
1. Giải phương trình: \(x^2+4x+3=0\)
2. Giải hệ phương trình: \(\left\{ \matrix{ x+y=4 \hfill \cr 3x -2y = 7 \hfill \cr} \right.\)
Câu 2: (2,0 điểm)
Cho biểu thức \(Q=(\frac{y\sqrt{y}+1}{y-1}-\frac{y-1}{\sqrt{y}-1}):(\sqrt{y}+\frac{\sqrt{y}}{\sqrt{y}-1})\) với \(y>0\) và \(y ≠1\)
1. Rút gọn \(Q\)
2. Tính giá trị của \(y\) khi \(Q=3\)
Câu 3: (2,0 điểm)
1. Cho hàm số \(y=mx+n \) \((m ≠0)\). Tìm m, n biết đồ thị hàm số song song với đường thẳng
\(y=-x+2018 \) (d) và đi qua điểm A(1;2018)
2. Tìm n để phương trình \(x^2-2(n-1)x-n-5=0\) có 2 nghiệm thoả mãn hệ thức \(x_1^2+x_2^2=14\)
Câu 4: (3,0 điểm)
Cho đường tròn (O;R), đường kính CD vuông góc với dây cung PQ tại điểm K (K nằm giữa O và D). Trên tia đối của tia QP lấy điểm E nằm ngoài đường tròn (O) sao cho đoạn thẳng CE cắt đường tròn (O) tại điểm H khác C. Hai dây PQ và DH cắt nhau ở M. Qua Q kẻ đường thẳng vuông góc với CE cắt tia PH tại N.
1. Chứng minh tứ giác CKMH nội tiếp
2. Chứng minh tam giác QNH cân và MP.QE = MQ.EP
3. Giả sử HM = HE. Chứng minh OH // PQ
Câu 5: (1,0 điểm)
Cho các số dương a, b, c thoả mãn: \(a+b+c=1\)
Chứng minh rằng: \(\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5\)
Vậy là cấu trúc đề thi thử vào 10 môn Toán của trường THCS Thị Trấn năm 2020 lần thứ nhất đều không có nhiều thay đổi so với cấu trúc đề tuyển sinh vào lớp 10 các năm. Hãy thử sức làm bài trong thời gian 120 phút rồi so sánh đối chiếu với lời giải chi tiết dưới đây sau em nhé.
Đáp án đề thi thử vào 10 năm 2020 môn Toán - THCS Thị Trấn
Câu 1: (2,0 điểm)
1. Giải phương trình: \(x^2+4x+3=0\)
\(\Leftrightarrow (x+1)(x+3)=0\)
\(\Leftrightarrow \left[ \matrix{ {x} = {-1} \hfill \cr {x} = {-3} \hfill \cr} \right. \)
Vậy phương trình có 2 nghiệm \(x=-1\) hoặc \(x=-3\)
2. Giải hệ phương trình: \(\left\{ \matrix{ x+y=4 \hfill \cr 3x -2y = 7 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ 2x+2y=8 \hfill \cr 3x -2y = 7 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ 2x+2y=8 \hfill \cr 5x = 15 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x=3 \hfill \cr y=1 \hfill \cr} \right.\)
Vậy phương trình có 1 nghiệm \((x;y)=(3;1)\)
Câu 2: (2,0 điểm)
Cho biểu thức \(Q=(\frac{y\sqrt{y}+1}{y-1}-\frac{y-1}{\sqrt{y}-1}):(\sqrt{y}+\frac{\sqrt{y}}{\sqrt{y}-1})\) với \(y>0\) và \(y ≠1\)
1. Rút gọn \(Q\)
Ta có:
\(Q=(\frac{y\sqrt{y}+1}{y-1}-\frac{y-1}{\sqrt{y}-1}):(\sqrt{y}+\frac{\sqrt{y}}{\sqrt{y}-1})\)
\(\Leftrightarrow Q=(\frac{(\sqrt{y}+1)(y-\sqrt{y}+1)}{(\sqrt{y}-1)(\sqrt{y}+1)}-\frac{y-1}{\sqrt{y}-1}):(\frac{y-\sqrt{y}+\sqrt{y}}{\sqrt{y}-1})\)
\(\Leftrightarrow Q=(\frac{y-\sqrt{y}+1}{\sqrt{y}-1}-\frac{y-1}{\sqrt{y}-1}):(\frac{y}{\sqrt{y}-1})\)
\(\Leftrightarrow Q=(\frac{y-\sqrt{y}+1-y+1}{\sqrt{y}-1}).(\frac{\sqrt{y}-1}{y})\)
\(\Leftrightarrow Q=(\frac{2-\sqrt{y}}{\sqrt{y}-1}).(\frac{\sqrt{y}-1}{y})=\frac{2-\sqrt{y}}{y}\)
Vậy \(Q=\frac{2-\sqrt{y}}{y}\)
2. Tính giá trị của \(y\) khi \(Q=3\)
Khi \(Q=3\) \(\Leftrightarrow Q=\frac{2-\sqrt{y}}{y} = 3\)
\(\Leftrightarrow 3y+\sqrt{y}-2 = 0\)
\(\Leftrightarrow (\sqrt{y}+1)(3\sqrt{y}-2)=0\)
\(\Rightarrow \) \(\sqrt{y} = -1\) (vô lý) hoặc \(\sqrt{y} =\frac{2}{3}\)\(\Leftrightarrow y =\frac{4}{9}\) (thoả mãn)
Vậy \(Q=3\)\(\Leftrightarrow y =\frac{4}{9}\)
Câu 3: (2,0 điểm)
1. Cho hàm số \(y=mx+n \) \((m ≠0)\). Tìm m, n biết đồ thị hàm số song song với đường thẳng
\(y=-x+2018 \) (d) và đi qua điểm A(1;2018)
Vì đồ thị hàm số đã cho song song với (d) \(\Rightarrow \) \(m=-1\)\(\Rightarrow \) phương trình đồ thị hàm số đã cho có dạng \(y=-x+n \)
Lại có, đồ thị hàm đã cho đi qua điểm A(1;2018) \(\Leftrightarrow 2018=-1+n\)\(\Leftrightarrow n=2019\)
Vậy \((m;n)=(-1;2019)\)
2. Tìm n để phương trình \(x^2-2(n-1)x-n-5=0\) (1) có 2 nghiệm thoả mãn hệ thức \(x_1^2+x_2^2=14\)
Để phương trình (1) có 2 nghiệm \(\Leftrightarrow \Delta' =(n-1)^2 - (-n-5) \geq 0\)
\(\Leftrightarrow \Delta' =n^2-n +6 \geq 0\)
Dễ thấy \(\Delta' > 0\) với mọi n nên phương trình đã cho luôn có 2 nghiệm phân biệt.
Áp dụng hệ thức Vi-ét cho (1), ta có:
\(\left\{ \matrix{ x_1+x_2=2(n-1) \hfill \cr x_1x_2=-n-5 \hfill \cr} \right.\) (*)
Ta có: \(x_1^2+x_2^2=14\)
\(\Leftrightarrow (x_1+x_2)^2-2x_1x_2=14\)
\(\Leftrightarrow 4(n-1)^2-2(-n-5)=14\)
\(\Leftrightarrow 4n^2-6n+14=14\)
\(\Leftrightarrow 4n^2-6n=0\)
\(\Leftrightarrow \left\{ \matrix{n=0 \hfill \cr n=\frac{3}{2} \hfill \cr} \right.\)
Vậy \(n=0\) hoặc \(n=\frac{3}{2}\) thì \(x_1^2+x_2^2=14\)
Câu 4: (3,0 điểm)
Cho đường tròn (O;R), đường kính CD vuông góc với dây cung PQ tại điểm K (K nằm giữa O và D). Trên tia đối của tia QP lấy điểm E nằm ngoài đường tròn (O) sao cho đoạn thẳng CE cắt đường tròn (O) tại điểm H khác C. Hai dây PQ và DH cắt nhau ở M. Qua Q kẻ đường thẳng vuông góc với CE cắt tia PH tại N.
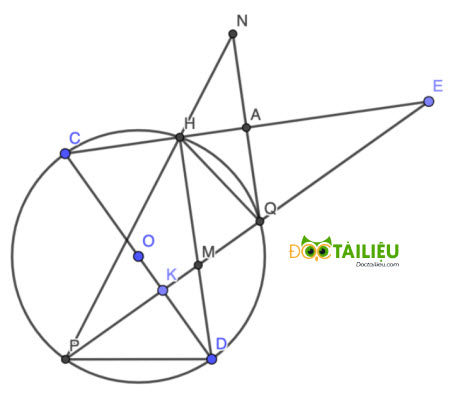
1. Chứng minh tứ giác CKMH nội tiếp
Dễ thấy \(\angle CKM = \angle CHM = 90⁰\) (gt) nên tứ giác CKMH nội tiếp (đpcm)
2. Chứng minh tam giác QNH cân và MP.QE = MQ.EP
D là điểm chính giữa cung nhỏ PQ (theo định lý đường kính và dây của đường tròn) => HD là phân giác trong của góc PHQ hay \(\angle PHD = \angle QHD\)
Lại có HM // QN (do cùng ⊥ CE) => \(\angle PHD = \angle PNQ \) và \(\angle QHD = \angle HQN \)
Từ 3 điều trên => \(\angle HNQ = \angle HQN\) => tam giác QNH cân tại H (đpcm)
Xét tam giác PQN có HM // QN => \(\frac{PM}{PQ}=\frac{HM}{QN}\) (1)
Tương tự với tam giác EHM có AQ // HM => \(\frac{EQ}{EM}=\frac{AQ}{HM}\) (2)
Nhân vế với vế (1) và (2), ta có: \(\frac{PM.EQ}{PQ.EM}=\frac{AQ}{QN}=\frac{1}{2}\)
\(\Leftrightarrow MP.QE=\frac{1}{2}PQ.EM\)\(=QK.EM\) (3)
Ta có \(\triangle MDP \sim \triangle MQH\) \(\Rightarrow \frac{MP}{MH}=\frac{MD}{MQ}\) \(\Rightarrow MP.MQ = MH.MD\)
\(\triangle MKD \sim \triangle MHE\) \(\Rightarrow \frac{MK}{MH}=\frac{MD}{ME}\) \(\Rightarrow MK.ME = MH.MD\)
Từ 2 điều trên \(\Rightarrow MK.ME = MP.MQ\)
\(\Leftrightarrow MK.ME+QM.ME = MP.MQ+QM.ME\)
\(\Leftrightarrow (MK+QM).ME = MQ.(MP+ME)\)
\(\Leftrightarrow QK.ME = MQ.EP\) (4)
Từ (3) và (4) \(\Leftrightarrow MP.QE = MQ.EP \) (đpcm)
3. Giả sử HM = HE. Chứng minh OH // PQ
Với HM = HE, ta dễ thấy tam giác MHE vuông cân tại H. Lại có \(\triangle MHE \sim \triangle MKD\) (2 tam giác vuông có góc đối đỉnh) \(\Rightarrow \angle DMK = \angle MDK = 45 ⁰\) hay \(\angle HDC = 45 ⁰\) hay tam giác DHC vuông cân tại H. Có HO là trung tuyến của tam giác DHC vuông cân tại H \(\Rightarrow HO ⊥ DC\)
Kết hợp với \( PQ ⊥ DC\) \(\Rightarrow HO{\space} // {\space}PQ\) (đpcm)
Câu 5: (1,0 điểm)
Cho các số dương a, b, c thoả mãn: \(a+b+c=1\)
Chứng minh rằng: \(\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5\)
Ta đi chứng minh bổ đề:
\(2a^2+ab+2b^2 \geq \frac{5}{4}(a+b)^2\) (1)
Thật vậy, (1) \(\Leftrightarrow 8a^2+4ab+8b^2 \geq 5(a+b)^2\)
\(\Leftrightarrow 8a^2+4ab+8b^2 \geq 5a^2+10ab+5b^2\)
\(\Leftrightarrow 3a^2-6ab+3b^2 \geq 0\)
\(\Leftrightarrow 3(a-b)^2 \geq 0\) Luôn đúng với mọi a và b hay ta có đpcm, tức là:
\(2a^2+ab+2b^2 \geq \frac{5}{4}(a+b)^2\)\(\Leftrightarrow \sqrt{2a^2+ab+2b^2} \geq \frac{\sqrt5}{2}(a+b)\)
Chứng minh tương tự, ta có:
\(\sqrt{2b^2+bc+2c^2} \geq \frac{\sqrt5}{2}(b+c)\) và
\(\sqrt{2c^2+ca+2a^2} \geq \frac{\sqrt5}{2}(c+a)\)
Cộng vế theo vế các bất đẳng thức trên, ta có:
\(\sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \frac{\sqrt5}{2}[(a+b)+(b+c)+(c+a)] = \sqrt5 (a+b+c) =\sqrt5\)
\(\Leftrightarrow \sqrt{2a^2+ab+2b^2}+\sqrt{2b^2+bc+2c^2}+\sqrt{2c^2+ca+2a^2} \geq \sqrt5\) (đpcm)
Dấu bằng xảy ra \(\Leftrightarrow a=b=c=\frac{1}{3}\)
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 trườngTHCS Thị Trấn lần 1, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn toán khác của các tỉnh thành trên cả nước nhé.
