Cùng Đọc tài liệu thử sức với đề thi khảo sát chất lượng môn Toán (chung) của trường THPT Chuyên Biên Hòa dành cho các em học sinh lớp 9 thi tuyển sinh vào 10 năm học 2020-2021:
Đề thi
Câu 1: (1,5 điểm)
Cho biểu thức:
\(P = \left( \dfrac{\sqrt{x}+2}{\sqrt x +3} - \dfrac{\sqrt{x}+1}{3 - \sqrt x } - \dfrac{2x+3}{x-9 } \right). \dfrac{x-9}{\sqrt x }\)
(\(x>0;x ≠9\))
1. Rút gọn biểu thức P
2. Tính giá trị của P khi \(x = 4-2\sqrt 3\)
Câu 2: (2,0 điểm)
1. Giải phương trình:
\(4x^2 - 5x - 9 = 0\)
2. Giải hệ phương trình:
\(\left\{ \matrix{ 2x^2-5y = -13 \hfill \cr 3x^2+y = 6 \hfill \cr} \right.\)
Câu 3: (1,5 điểm)
Cho hàm số \(y=x^2\) có đồ thị là parabol (P) và hàm số \(y=2mx-6m+9\) có đồ thị là đường thẳng (d).
1. Tìm m để (d) tiếp xúc với (P).
2. Tìm m để (d) cắt (P) tại hai điểm phân biệt A(x1;y1), B(x2;y2) sao cho \(y_1 + 2{mx}_2 -3m - 18 = 0\)
Câu 4: (4 điểm)
Cho điểm M nằm ngoài đường tròn (O). Từ M kẻ hai tiếp tuyến MA, MB (A, B là các tiếp điểm). Qua M kẻ một đường thẳng không đi qua O cắt đường tròn tại hai điểm C, D (C nằm giữa M và D). Gọi H là trung điểm của CD, K là giao điểm của AB và MO.
1. Chứng minh rằng 5 điểm M, A, H, O, B cùng thuộc một đường tròn.
2. Chứng minh MC.MD = MK.MO
3. Qua C kẻ đường thẳng song song với MA cắt AB và AD lần lượt tại E và F. Chứng minh tứ giác CEHB nội tiếp và E là trung điểm của CF.
4. Gọi G là giao điểm của MF và AC. Chứng minh rằng D, E, G thẳng hàng.
Câu 5: (1,0 điểm)
Cho các số thực dương a,b,c thoả mãn abc = 1. Chứng minh rằng:
\(\dfrac{1}{(1+a)^2} + \dfrac{1}{(1+b)^2} + \dfrac{1}{(1+c)^2} + \dfrac{2}{(1+a)(1+b)(1+c)} \geq 1\)
Hết
Xem thêm các tài liệu đề thi thử vào lớp 10 tất cả các môn khác nữa em nhé!
Lời giải chi tiết
Câu 1: (1,5 điểm)
1.
Với \(x>0;x ≠9\), ta có:
\(P = \left( \dfrac{\sqrt{x}+2}{\sqrt x +3} - \dfrac{\sqrt{x}+1}{3 - \sqrt x } - \dfrac{2x+3}{x-9 } \right). \dfrac{x-9}{\sqrt x }\)
\(= \left[ (\sqrt{x}+2)(\sqrt{x}-3)+ (\sqrt{x}+1)(\sqrt{x}+3) -(2x+3) \right]. \dfrac{1}{\sqrt x }\)
\(= \left( x-\sqrt{x}-6 +x + 4\sqrt{x}+3 -2x-3 \right). \dfrac{1}{\sqrt x }\)
\(= \dfrac{3\sqrt x -6}{\sqrt x }\)
2.
Ta có:
\(x = 4-2\sqrt 3\) \(= 3-2.1.\sqrt 3 + 1\)
\(= (\sqrt 3 - 1)^2\)\(\Rightarrow \sqrt x = \sqrt 3 -1\)
Thay vào P ta có:
\(P = \dfrac{3\sqrt x -6}{\sqrt x } \) \(= \dfrac{3(\sqrt 3 -1) -6}{\sqrt 3 -1 }\) \(= \dfrac{3\sqrt 3 -9}{\sqrt 3 -1 }\) \(= \dfrac{(3\sqrt 3 -9)(\sqrt 3 +1)}{2 }\) \(= -3\sqrt 3\)
Câu 2: (2,0 điểm)
1. Giải phương trình:
\(4x^2 - 5x - 9 = 0\)
\(\Leftrightarrow \left[ \matrix{ x_1 = -1 \hfill \cr x_2 = \dfrac{9}{4} \hfill \cr} \right.\)
2. Giải hệ phương trình:
\(\left\{ \matrix{ 2x^2-5y = -13 \hfill \cr 3x^2+y = 6 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x^2 = 1 \Leftrightarrow x =±1 \hfill \cr y = 3 \hfill \cr} \right.\)
Câu 3: (1,5 điểm)
Cho hàm số \(y=x^2\) có đồ thị là parabol (P) và hàm số \(y=2mx-6m+9\) có đồ thị là đường thẳng (d).
1. Tìm m để (d) tiếp xúc với (P).
Để (d) tiếp xúc với (P) ⇔ phương trình sau có một nghiệm duy nhất:
\(x^2=2mx-6m+9\)
⇔ \(x^2 - 2mx + 6m - 9 = 0\)
\(\Delta' = m^2 - 6m + 9 = (m-3)^2\)
Để phương trình trên có nghiệm duy nhất ⇔ \(\Delta' = 0\) ⇔ \(m=3\).
Vậy để (d) tiếp xúc với (P) ⇔ \(m=3\).
2. \(y_1 + 2{mx}_2 -3m - 18 = 0\) (*)
Hoành độ của A và B là nghiệm của phương trình:
\(x^2=2mx-6m+9\)
⇔ \(x^2 - 2mx + 6m - 9 = 0\)
Để (d) cắt (P) tại 2 điểm phân biệt ⇔
\(\Delta' = m^2 - 6m + 9 = (m-3)^2 > 0\)
⇔ \(m ≠ 3\)
Áp dụng hệ thức Vi-ét cho phương trình trên, ta có:
\(\left\{ \matrix{ x_1+x_2 = 2m \hfill \cr x_1x_2=6m-9 \hfill \cr} \right.\)
Ta có điểm A thuộc (d) nên:
\(y_1=2mx_1-6m+9\)
Thay vào phương trình (*) ta có:
\(2mx_1-6m+9 + 2{mx}_2 -3m - 18 = 0\)
\(\Leftrightarrow 2m(x_1+x_2) -9m - 9 = 0\)
\(\Leftrightarrow 4m^2-9m - 9 = 0\)
\(\Leftrightarrow \left[ \matrix{ m = 3\hfill \cr m = \dfrac{-3}{4} \hfill \cr} \right.\)
Kết hợp với điều kiện để (d) cắt (P) tại 2 điểm phân biệt hay \(m ≠ 3\) \(\Rightarrow m = \dfrac{-3}{4}\).
Câu 4: (4 điểm)
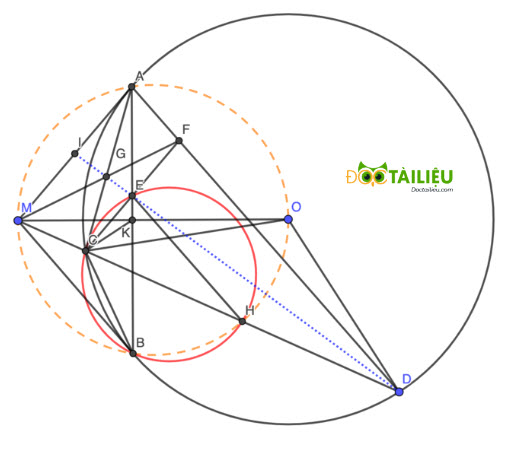
1.
Vì MA, MB là tiếp tuyến tới (O) tại A và B ⇒ ∠MAO = ∠MBO = 90⁰ (1)
Vì H là trung điểm CD ⇒ OH ⊥ CD (tính chất dây cung) hay ∠MHO = 90⁰ (2)
Từ (1) và (2) suy ra A, B, H cùng thuộc đường tròn đường kính OM, hay 5 điểm M, A, H, O, B cùng thuộc một đường tròn (đpcm).
2.
Theo tính chất tiếp tuyến, ta có OM ⊥ AB.
Xét △MAK và △MOA có:
∠MAO = ∠MKA = 90⁰
Góc ∠OMA chung
Suy ra △MAK ∽ △MOA ⇒ \(\dfrac{MA}{MK} = \dfrac{MO}{MA} \) ⇒ MK.MO = MA² (3)
Xét △MAC và △MDA có:
∠CAM = ∠CDA (t/c góc tạo bởi tiếp tuyến và dây cung)
Góc ∠AMD chung
Suy ra △MAC ∽ △MDA ⇒ \(\dfrac{MA}{MC} = \dfrac{MD}{MA} \) ⇒ MC.MD = MA² (4)
Từ (3) và (4) suy ra MC.MD = MK.MO (đpcm).
3.
Vì 5 điểm M, A, O, H, B cùng thuộc một đường tròn ⇒ ∠AMH = ∠ABH = ∠EBH
Lại có CE // AM (gt) ⇒ ∠AMH = ∠ECH (góc đồng vị)
Suy ra ∠EBH = ∠ECH ⇒ Tứ giác CEHB nội tiếp (đpcm).
⇒ ∠BCH = ∠BEH
Lại có ∠BCH = ∠BCD = ∠BAD
Suy ra ∠BEH = ∠BAD ⇒ EH // AD (góc đồng vị)
Xét △GAD có H là trung điểm GD và EH // AD ⇒ EH là đường trung bình của △GAD ⇒ E là trung điểm CF (đpcm).
4.
Gọi DE cắt AM tại I. Vì DF // MA ⇒ \(\dfrac{CE}{MI} = \dfrac{DE}{DI} =\dfrac{EF}{IA} \)
Mà CE = EF (do E là trung điểm của CF) ⇒ MI = IA hay I là trung điểm MA.
Tương tự, Gọi EG cắt AM tại I'. Vì DF // MA ⇒ \(\dfrac{CE}{AI'} = \dfrac{GE}{GI'} =\dfrac{EF}{I'M} \)
Mà CE = EF (do E là trung điểm của CF) ⇒ MI' = I'A hay I' là trung điểm MA hay I' ≡ I hay I, G, E, D thẳng hàng (đpcm).
Câu 5: (1,0 điểm)
Ta đặt:
\(P = \dfrac{1}{(1+a)^2} + \dfrac{1}{(1+b)^2} + \dfrac{1}{(1+c)^2} + \dfrac{2}{(1+a)(1+b)(1+c)} \)
Trong ba số a,b,c có tích bằng 1 nên luôn tồn tại hai số nằm về cùng một phía với 1. Giả sử là a và b. Ta có:
\((1-a)(1-b) \geq 0\)
\(\Leftrightarrow a+b \leq 1+ab = 1 + \dfrac{1}{c} = \dfrac{1+c}{c}\)
Và:
\((1+a)(1+b)(1+c) = (1+a+b+ab)(1+c) \leq 2(1+ab)(1+c)\)
\(\Leftrightarrow (1+a)(1+b)(1+c) \leq \dfrac{2(1+c)^2}{c}\)
\(\Leftrightarrow \dfrac{2}{(1+a)(1+b)(1+c)} \geq \dfrac{c}{(1+c)^2}\) (1)
Áp dụng BĐT Cauchy - Schwarz cho bộ số \((1;a)\) và \((1;ab)\), ta có:
\(\dfrac{1^2}{1} + \dfrac{a^2}{ab} \geq \dfrac{(1+a)^2}{1+ab} \)
\(\Leftrightarrow ({1+ab} )(1 + \dfrac{a}{b}) \geq {(1+a)^2}\)
\(\Leftrightarrow \dfrac{1}{(1+a)^2} \geq \dfrac{1}{(1+ab)(1+\frac{a}{b})} \)
Tương tự, ta được:
\(\dfrac{1}{(1+a)^2} + \dfrac{1}{(1+b)^2} \geq \dfrac{1}{(1+ab)(1+\frac{a}{b})} +\dfrac{1}{(1+ab)(1+\frac{b}{a})}\)
\(\Leftrightarrow \dfrac{1}{(1+a)^2} + \dfrac{1}{(1+b)^2} \geq \dfrac{b}{(1+ab)(b+a)} +\dfrac{a}{(1+ab)(a+b) } \)
\(\Leftrightarrow \dfrac{1}{(1+a)^2} + \dfrac{1}{(1+b)^2} \geq \dfrac{1}{1+ab} = \dfrac{c}{c+1}\) (2)
Từ (1) và (2) suy ra:
\(P \geq \dfrac{c}{c+1} + \dfrac{1}{(c+1)^2} + \dfrac{c}{(c+1)^2}\)
\(\Leftrightarrow P \geq \dfrac{c(c+1)+1+c}{(c+1)^2} = 1\) (đpcm)
Dấu bằng xảy ra \(\Leftrightarrow a=b=c=1\).
-/-
Nếu em có mong muốn thi vào 10 chuyên Toán - Chuyên Biên Hòa thì đừng quên xem thêm: Đề thi thử vào lớp 10 môn Toán chuyên 2020 của THPT Chuyên Biên Hoà
Trên đây là đề thi thử vào 10 môn toán (chung) năm 2020 do trường THPT Chuyên Biên Hòa ra đề, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
