Cùng Đọc tài liệu thử sức với đề thi thử tuyển sinh vào lớp 10 môn toán năm 2020 tại Quảng Ninh nhé:
Đề thi thử
Bài I (1,5 điểm)
1) Tính giá trị của biểu thức
\(A = \dfrac{\sqrt x +1}{\sqrt x -1}\)
khi x = 9.2) Cho biểu thức:
\(P = \left( \dfrac{x-2}{x+2\sqrt x} + \dfrac{1}{\sqrt x + 2} \right) . \dfrac{\sqrt x + 1}{\sqrt x -1} \)
Với \(x > 0; x ≠ 1\).
a) Rút gọn P.
b) Tìm tất cả các giá trị nguyên của x để P đạt giá trị nguyên.
Bài II (1,5 điểm)
Giải các phương trình và hệ phương trình sau:
a) \(x^2 - 7x + 12 = 0\)
b) \(x^4 - 9x^2 + 20 = 0\)
c) \(\left\{ \matrix{ 3x - 2y = 4 \hfill \cr 4x - 3y= 5 \hfill \cr} \right.\)
Bài III (2,0 điểm)
Trên mặt phẳng toạ độ Oxy cho đường thẳng (d) và parabol (P):
(d): \(y = -x + 6\)
(P): \(y = x^2\)
a) Vẽ (d) và (P) trên cùng một mặt phẳng toạ độ.
b) Tìm toạ độ các giao điểm của (d) và (P) bằng phép tính.
c) Gọi A, B là hai giao điểm của (d) và (P). Tính diện tích tam giác OAB.
Bài IV (2,0 điểm)
Giải bài toán bằng cách lập phương trình:
Một phân xưởng theo kế hoạch cần phải sản xuất 1100 sản phẩm trong một số ngày quy định. Do mỗi ngày phân xưởng đó sản xuất vượt mức 5 sản phẩm nên phân xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định 2 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải sản xuất bao nhiêu sản phẩm?
Bài V (3,0 điểm)
Cho nửa đường tròn (O) đường kính AB = 2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tuỳ ý (M khác A và B), tia AM cắt d tại N. Gọi C là trung điểm của AM, tia CO cắt d tại D.
a) Chứng minh rằng OBNC nội tiếp.
b) Chứng minh rằng NO ⊥ AD.
c) Chứng minh rằng CA.CN = CO.CD.
d) Xác định vị trí điểm M để (2AM + AN) đạt giá trị nhỏ nhất.
Hết
Trên đây là 5 câu hỏi trong đề thi thử tuyển sinh vào lớp 10 mã đề 01 của THCS Bình Dương (TX Đông Triều - Quảng Ninh) với môn Toán, cùng làm bài thi này trong 120 phút rồi đối chiếu với đáp án chi tiết dưới đây em nhé:
Đáp án
Bài I:
1)
Thay x = 9 vào A ta có:
\(A = \dfrac{\sqrt x +1}{\sqrt x -1} = \dfrac{\sqrt 9 +1}{\sqrt 9 -1} = 2\)
2) Cho biểu thức:
\(P = \left( \dfrac{x-2}{x+2\sqrt x} + \dfrac{1}{\sqrt x + 2} \right) . \dfrac{\sqrt x + 1}{\sqrt x -1} \)
a)
Với \(x > 0; x ≠ 1\), ta có:
\(P = \left( \dfrac{x-2}{x+2\sqrt x} + \dfrac{1}{\sqrt x + 2} \right) . \dfrac{\sqrt x + 1}{\sqrt x -1} \)
\( = \dfrac{x-2+ \sqrt x}{\sqrt x(\sqrt x+2)} . \dfrac{\sqrt x + 1}{\sqrt x -1} \)
\( = \dfrac{(\sqrt x-1)(\sqrt x+2)}{\sqrt x(\sqrt x+2)} . \dfrac{\sqrt x + 1}{\sqrt x -1} \)
\( = \dfrac{\sqrt x + 1}{\sqrt x } \)
b)
Để P nguyên \(\Leftrightarrow \dfrac{\sqrt x + 1}{\sqrt x } = 1 + \dfrac{1}{\sqrt x } \) là số nguyên
\(\Leftrightarrow \dfrac{1}{\sqrt x } \) là số nguyên.
\(\Rightarrow \dfrac{1}x ∈ ℤ \Rightarrow x = ±1\).
Mà \(x > 0; x ≠ 1\) \(\Rightarrow\) không tồn tại giá trị nguyên của x để P nguyên.
Bài II:
a) \(x^2 - 7x + 12 = 0\)
\(\Leftrightarrow \left[ \matrix{ {x} = 3\hfill \cr {x} =4 \hfill \cr} \right. \)
b) \(x^4 - 9x^2 + 20 = 0\)
\(\Leftrightarrow \left[ \matrix{ x^2 = 5\hfill \cr x^2 =4 \hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{ x = ± \sqrt 5\hfill \cr x = ± 2 \hfill \cr} \right. \)
c) \(\left\{ \matrix{ 3x - 2y = 4 \hfill \cr 4x - 3y= 5 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{ x=2 \hfill \cr y= 1 \hfill \cr} \right.\)
Bài III:
a) Vẽ (d) và (P) trên cùng một mặt phẳng toạ độ.
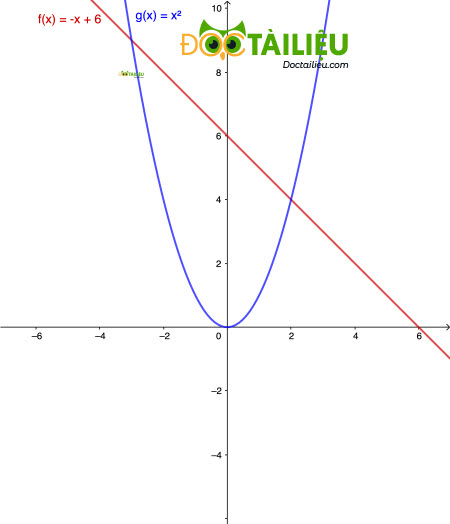
b)
Phương trình hoành độ giao điểm của (d) và (P) là:
\(x^2 = -x + 6 \Leftrightarrow x^2 + x -6 = 0\)
\(\Leftrightarrow \left[ \matrix{ x = 2 \Rightarrow y = 4\hfill \cr x = -3 \Rightarrow y = 9 \hfill \cr} \right. \)
c)
Từ phần b ta có A(2;4) và B(-3;9). Ta có:
\(S_{\triangle OAB} = \dfrac{1}2 d_{(O;d)}.AB = \dfrac{1}2.\dfrac{6}{\sqrt{1+1}}.\sqrt{(2+3)^2+(4-9)^2} = 15\)
Bài IV:
Gọi số sản phẩm mỗi ngày phân xưởng phải sản xuất theo kế hoạch là A (A ∈ ℕ*).
Số ngày quy định là \(\dfrac{1100}A\) (ngày)
Theo giả thiết ta có:
\(\dfrac{1100}A -2= \dfrac{1100}{A+5} \)
\(\Leftrightarrow 2A^2 + 10 A - 5500 = 0\)
\(\Leftrightarrow \left[ \matrix{ A = 50 \space (tm) \hfill \cr A = -55 \space (loại) \hfill \cr} \right. \)
Bài V:
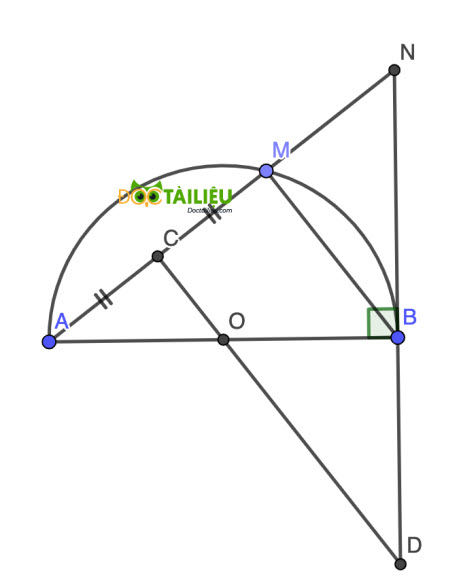
a)
Xét △OMA có OA = OM = R ⇒ △OMA cân tại O. Có C là trung điểm AM ⇒ OC đồng thời là đường cao hay OC ⊥ AM hay ∠OCN = 90°.
Lại có NB là tiếp tuyến của (O) tại B ⇒ ∠OBN = 90° = ∠OCN ⇒ C và B cùng thuộc đường tròn đường kính NC hay tứ giác OBNC nội tiếp (đpcm).
b)
Xét △NAD có AB ⊥ ND, DC ⊥ AN và AB cắt DC tại O ⇒ O là trực tâm của △NAD hay NO ⊥ AD (đpcm).
c)
Xét △COA và △CND có:
∠ACO = ∠NCD ( = 90°)
∠CAO = 90° - ∠ANB = ∠CDN
Suy ra △COA ∽ △CND ⇒ \(\dfrac{CO}{CA} = \dfrac{CN}{CD} \) ⇒ CA.CN = CO.CD (đpcm).
d)
Xét △AMB và △ABN có:
Góc MAB chung
∠ABN = 90° = ∠AMB (do M nội tiếp chắn đường kính AB)
Suy ra △AMB ∽ △ABN ⇒ \(\dfrac{AM}{AB} = \dfrac{AB}{AN} \) ⇒ AM.AN = AB² = 4R².
Áp dụng BĐT AM-GM ta có:
\(2AM + AN \geq 2\sqrt{2AM.AN} = 4\sqrt 2 R\).
Vậy \({Min}_{2AM+AN} = 4\sqrt 2 R \Leftrightarrow 2AM = AN \) hay M là trung điểm AN, hay M là điểm chính giữa cung AN.
-/-
Trên đây là hướng dẫn giải chi tiết đề thi thử vào 10 môn toán năm 2020 THCS Bình Dương (TX Đông Triều - Quảng Ninh), mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
