Cùng Đọc tài liệu thử sức với đề thi thử vào lớp 10 môn toán năm 2020-2021 của trường Lương Thế Vinh, TP.HCM để chuẩn bị tốt nhất cho kỳ thi vào 10 sắp tới.
Đề thi thử vào 10 môn toán 2021 Lương Thế Vinh HCM
Câu 1:
Giải các phương trình và hệ phương trình sau:a) \((x-3)^{2}-7 x=2 x(x+3)-33\)
b) \(5 x^{2}-2 \sqrt{10} x+2=0\)
c) \(x^{4}-2 x^{2}-8=0\)
d) \(\left\{\begin{array}{l}2(x+1)=-3 y \\ 3 x-5 y=-3(1+y)\end{array}\right.\)
Câu 2:
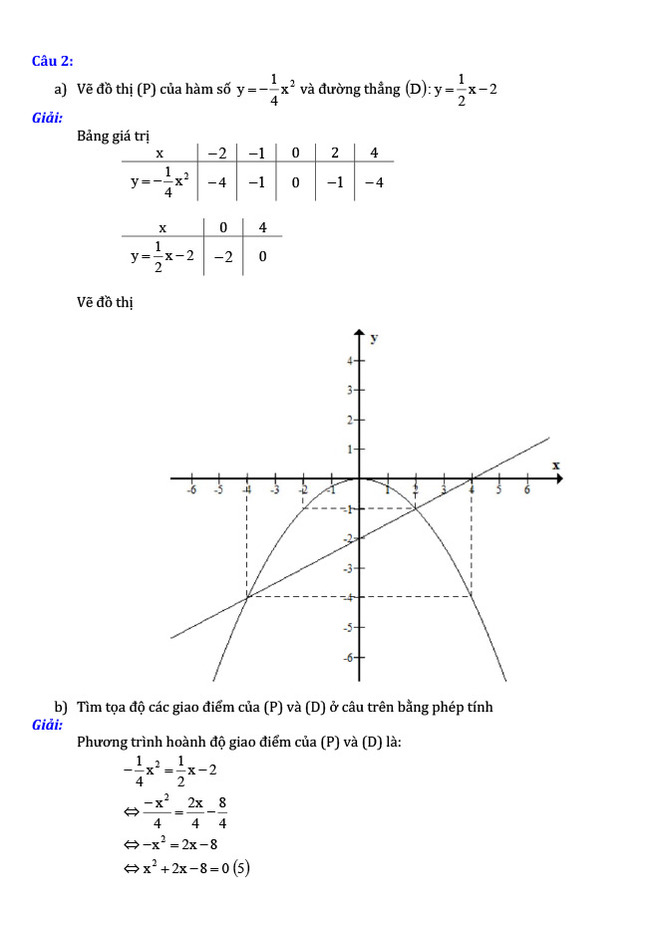
a) Vẽ đồ thị (P) của hàm số \({y}=-\dfrac{1}{4} {x}^{2}\) và đường thẳng (P): \({y}=\dfrac{1}{2} {x}-2\)
b) Tìm tọa độ các giao điểm của (P) và (D) ở câu trên bằng phép tính
Câu 3: Thu gọn biểu thức:
\(A=\frac{\sqrt{\sqrt{10}-3}-\sqrt{2}-\sqrt{\sqrt{10}+3}}{\sqrt{2}}+\sqrt{\sqrt{10}-1}\)
Câu 4: Cho phương trình: \(x^{2}-(2 m-1) x+m^{2}+m-3=0 (1)\) (x là ẩn số)
a) Xác định m để phương trình (1) có hai nghiệm phân biệt \(x_1; x_2\)
b) Xác định m để: \({x}_{1}({x}_{1}-1)+{x}_{2}({x}_{2}-1)=18\)
Câu 5: Cho đường tròn (O; R) và điểm M nằm ngoài (O). Vẽ 2 tiếp tuyến MA, MB và cát tuyến MCD của (O) (A, B là tiếp điểm, C nằm giữa M và D; A và C nằm khác phía đối với đường thẳng M0). Gọi I là trung điểm CD
a) Chứng minh: MB² = MC.MD
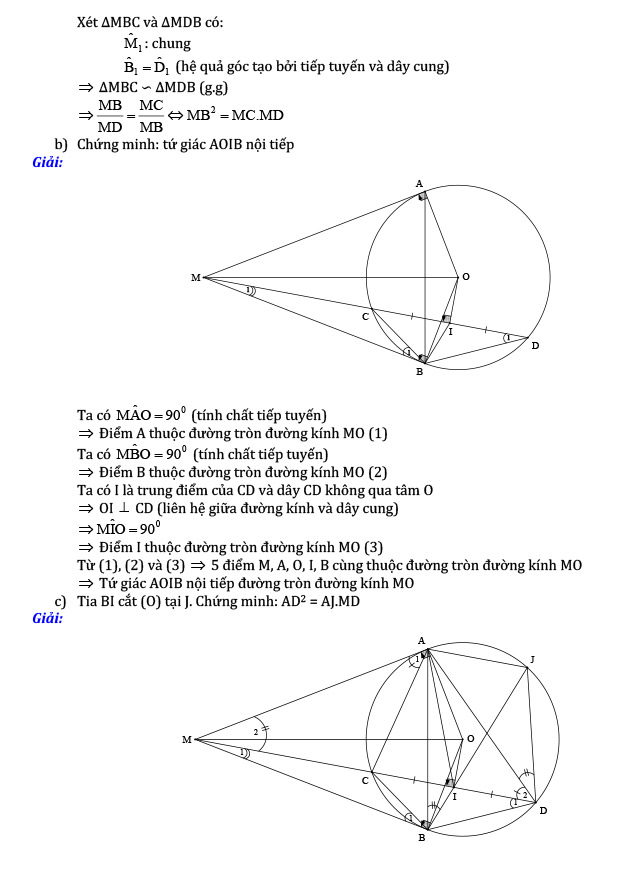
b) Chứng minh: tứ giác AOIB nội tiếp
c) Tia Bị cắt (O) tại J. Chứng minh: AD² = AJ.MD
d) Đường thẳng qua I song song với DB cắt AB tại K, tia CK cắt OB tại G. Tính bán kính đường tròn ngoại tiếp △CIG theo R
Câu 6: Hàng tháng một người gửi vào ngân hàng 5.000.000đ với lãi suất 0,6%/tháng. Hỏi sau 15 tháng người đó nhận được số tiền cả gốc lẫn lãi là bao nhiêu? Biết rằng hàng tháng người đó không rút lãi ra.
HẾT
Đáp án đề thi thử vào 10 môn toán 2021 Lương Thế Vinh HCM




-/-
Trên đây là chi tiết đề thi thử vào 10 môn toán năm 2021 của trường Lương Thế Vinh HCM mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào 10 môn Toán 2021 khác của các tỉnh thành trên cả nước nhé.
