Cùng Đọc tài liệu thử sức với đề thi khảo sát chất lượng môn Toán của Quận Long Biên dành cho các em học sinh lớp 9 thi tuyển sinh vào 10 năm học 2020-2021 tại Hà Nội:
Đề thi
UBND QUẬN LONG BIÊN PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC | ĐỀ KIỂM TRA KHẢO SÁT CHẤT LƯỢNG MÔN: TOÁN 9 Thời gian 120 phút Ngày thi: 10/6/2020 |
Bài 1: (2 điểm)
Cho hai biểu thức \(A = \dfrac{\sqrt{x}+5}{\sqrt{x}-3} \)và \(B = \dfrac{4}{\sqrt{x}+3} + \dfrac{2x-\sqrt{x}-13}{x-9}- \dfrac{\sqrt{x}}{\sqrt{x}-3}\)a) Tính giá trị của biểu thức A khi x = 4
b) Đặt \(P = \dfrac{B}{A}\). Chứng minh P = \(\dfrac{\sqrt{x}-5}{\sqrt{x}+3}\)
c) Tìm giá trị của x nguyên nhỏ nhất để P có giá trị nguyên.
Bài 2: (2,5 điểm) Bài toán liên quan đến ứng dụng toán học vào thực tế
1. Đề ủng hộ các gia đình gặp khó khăn tại địa phương do ảnh hưởng của dịch Covid-19, một tổ chức thiện nguyện đã dự kiến chở 720 tạ gạo chia đều bằng một số xe cùng loại. Lúc sắp khởi hành, do được bổ sung thêm 2 xe cùng loại; vì vậy so với dự định, mỗi xe chở ít đi 18 tạ gạo. Hỏi lúc đầu ban tổ chức đã chuẩn bị bao nhiêu xe chở gạo?
2. Thùng rác inox hình trụ tròn nắp lật xoay được sử dụng khá phổ biến do nắp được thiết kế có trục quay, mang đến khả năng tự cân bằng trở về trạng thái ban đầu sau khi bó rác. Biết thùng có đường kính đáy 40cm và chiều cao 60cm. Hãy tính diện tích Inox để làm ra chiếc thùng rác trên ( coi các mép gấp khi làm thùng không đáng kể) (hình minh họa)

Bài 3: (2 điểm)
1. Giải hệ phương trình:
\(\left\{ \matrix{ 3(x-2) - \dfrac{2}{y+3} = 4 \hfill \cr 2(x-2) + \dfrac{1}{y+3} = 5 \hfill \cr} \right.\)
2. Cho parabol (P): \(y= \dfrac{1}{2}x^2\) và đường thẳng (d): \(y = (m + 1)x - m\) (m là tham số, x là ẩn )
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi m.
b) Gọi x₁, x₂ là hoành độ giao điểm của (d) và (P). Tìm m để \(\sqrt{x_1}+\sqrt{x_2} = \sqrt{2}\).
Bài 4: (3 điểm) Cho đường tròn (O; R), đường kính AB và CD vuông góc với nhau. Điểm M di động trên cung nhỏ BC. Gọi N, E lần lượt là giao điểm của AM với CD, CB. Tia CM cắt AB tại S, MD cắt AB tại F. Kẻ CH vuông góc với AM tại H.
a) Chứng minh bốn điểm A, C, H, O cùng thuộc một đường tròn.
b) Chứng minh: SM.SC = SA.SB = SO.SF.
c) Chứng minh OH // DM và tỉa OH là tia phân giác của góc COM.
d) Chứng minh diện tích tứ giác ANFD không phụ thuộc vào vị trí điểm M di động trên cung nhỏ BC.
Bài 5 (0,5 điểm). Cho x, y, z là các số dương thỏa mãn x + y + z= 2020.
Tìm giá trị lớn nhất của biểu thức:
\(P = \dfrac{xy}{\sqrt{2020z+xy}} + \dfrac{yz}{\sqrt{2020x+yz}}+ \dfrac{zx}{\sqrt{2020y+zx}}\)
Hết
Vậy là Đọc tài liệu đã giới thiệu thêm cho các em một đề thi thử vào 10 tại Hà Nội, nhớ xem thêm các tài liệu đề thi thử vào lớp 10 tất cả các môn khác nữa em nhé!
Lời giải chi tiết
Lời giải:
Bài 1: (2 điểm)
a)
Thay x = 4 vào A, ta có:
\(A = \dfrac{\sqrt{x}+5}{\sqrt{x}-3} = \dfrac{\sqrt{4}+5}{\sqrt{4}-3} = -7\)
b)
ĐKXĐ: \(x\geq 0; x ≠ 9\)
Ta có:
\(P = \dfrac{B}{A}\) \( =\left( \dfrac{4}{\sqrt{x}+3} + \dfrac{2x-\sqrt{x}-13}{x-9}- \dfrac{\sqrt{x}}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}+5}{\sqrt{x}-3} \)
\( =\left[\dfrac{4(\sqrt{x}-3)+2x-\sqrt{x}-13-\sqrt{x}(\sqrt{x}+3)}{(\sqrt{x}-3)(\sqrt{x}+3)}\right].\dfrac{\sqrt{x}-3}{\sqrt{x}+5} \)
\( =\dfrac{x-25}{(\sqrt{x}+5)(\sqrt{x}+3)}\) \( =\dfrac{\sqrt{x}-5}{\sqrt{x}+3}\) (đpcm)
c)
ĐKXĐ: \(x\geq 0; x ≠ 9\)
Ta có:
\(P = \dfrac{\sqrt{x}-5}{\sqrt{x}+3}\) \(= 1-\dfrac{8}{\sqrt{x}+3}\)
Để P nguyên \(\Leftrightarrow \) \(8⋮(\sqrt x +3)\) \(\Rightarrow (\sqrt x + 3) \in \{±1;±2;±4;±8\}\)
Mà để x nhỏ nhất, thoả mãn ĐKXĐ \(\Leftrightarrow x = 1\).
Kết luận......
Bài 2: (2,5 điểm)
1.
Gọi số xe ban đầu tổ chức chuẩn bị là A (xe, A ∈ ℕ*)
Số gạo mỗi xe phải chở theo dự kiến ban đầu: \(\dfrac{720}{A}\)
Số gạo mỗi xe phải chở sau khi bổ sung: \(\dfrac{720}{A+2}\)
Theo giả thiết ta có:
\(\dfrac{720}{A} - \dfrac{720}{A+2} =18 \)
\(\Leftrightarrow 18 A^2 +36 A - 1440 = 0\)
Kết hợp với điều kiện A dương \(\Rightarrow A = 8 \) (xe).
2.
Ta thấy diện tích Inox để làm ra chiếc thùng rác này chính là diện tích toàn phần của hình trụ:
\(S_{tp} = 2 π \times r \times (r + h)\)
\(= 2 π \times 40\times (40 +60) = 8000 \pi\)(cm²)

Bài 3: (2 điểm)
1. Giải hệ phương trình:
\(\left\{ \matrix{ 3(x-2) - \dfrac{2}{y+3} = 4 \hfill \cr 2(x-2) + \dfrac{1}{y+3} = 5 \hfill \cr} \right.\) (đkxđ \(y≠-3\))
\(\Leftrightarrow \left\{ \matrix{ x-2=2 \hfill \cr \dfrac{1}{y+3} = 1 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x=4 \hfill \cr y = -2 \hfill \cr} \right.\)
2. Cho parabol (P): \(y= \dfrac{1}{2}x^2\) và đường thẳng (d): \(y = (m + 1)x - m\) (m là tham số, x là ẩn )
a)
Xét phương trình hoành độ giao điểm của (d) và (P), ta có:
\(\dfrac{1}{2}x^2 = (m + 1)x - m\) (*)
\(\Leftrightarrow x^2 - 2(m + 1)x +2 m =0\) (**)
\(\Delta' = (m+1)^2 - 2m = m^2 + 1 > 0\) với mọi m
Suy ra phương trình (*) luôn có hai nghiệm phân biệt, hay (d) luôn cắt (P) tại hai điểm phân biệt với mọi m (đpcm).
b)
Để \(\sqrt{x_1}+\sqrt{x_2} = \sqrt{2}\) tồn tại \(\Leftrightarrow \) phương trình (**) có hai nghiệm \(x_1;x_2 \geq 0\)
\(\Leftrightarrow \left\{ \matrix{ x_1+x_2 \geq 0 \hfill \cr x_1x_2 \geq 0 \hfill \cr} \right.\)
Áp dụng hệ thức Vi-et cho (**), ta có:
\( \left\{ \matrix{ x_1+x_2=2(m+1) \hfill \cr x_1x_2=2m \hfill \cr} \right.\) \(\Rightarrow m \geq 0\)
Ta có:
\(\sqrt{x_1}+\sqrt{x_2} = \sqrt{2}\)
\(\Leftrightarrow (\sqrt{x_1}+\sqrt{x_2})^2 = 2\)
\(\Leftrightarrow ({x_1}+{x_2})+ 2\sqrt{x_1x_2}= 2\)
\(\Leftrightarrow 2(m+1)+ 2\sqrt{2m}= 2\)
\(\Leftrightarrow 2m+ 2\sqrt{2m}= 0\)
\(\Leftrightarrow m= 0\) (do \(m \geq 0\))
Kết luận để \(\sqrt{x_1}+\sqrt{x_2} = \sqrt{2}\) \(\Leftrightarrow m= 0\)
Bài 4: (3 điểm)
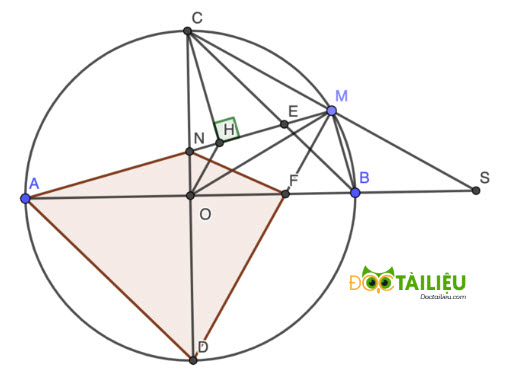
a)
Vì CH ⊥ AM và CD ⊥ AB (theo gt) ⇒ ∠CHA = ∠COA = 90⁰ ⇒ H, O cùng thuộc đường tròn đường kính CA hay bốn điểm A, C, H, O cùng thuộc một đường tròn (đpcm).
b)
Vì tứ giác ACMB nội tiếp (O) ⇒ ∠CAB = 180⁰ - ∠CMB = ∠BMS.
Xét △SMB và △SAC, ta có:
Góc ∠BSM chung
∠CAB = ∠BMS (cmt)
Suy ra △SMB ∽ △SAC ⇒ \(\dfrac{SM}{SB} = \dfrac{SA}{SC}\) ⇒ SM.SC = SA.SB (1).
Xét △SMF và △SOC, ta có:
Góc ∠CSO chung
∠COS = ∠FMS = 90⁰ (Góc M chắn đường kính CD nội tiếp (O))
Suy ra △SMF ∽ △SOC ⇒ \(\dfrac{SM}{SF} = \dfrac{SO}{SC}\) ⇒ SM.SC = SO.SF (2).
Từ (1) và (2) ⇒ SM.SC = SA.SB = SO.SF (đpcm).
c)
Vì tứ giác ACHO nội tiếp (cm phần a) ⇒ ∠COH = ∠CAH (cùng chắn cung CH) = ∠CDM (nội tiếp (O) chắn cung CM) Hay ∠COH = ∠CDM ⇒ OH // DM (đồng vị) (đpcm).
Mà lại có DM ⊥ CM ⇒ OH ⊥ CM.
Xét △OCM có OC = OM = R ⇒ △OCM cân tại O, có OH ⊥ CM suy ra OH đồng thời là tia phân giác góc COM (đpcm).
d)
Ta thấy:
\(S_{ANFD} = S_{ANF} + S_{ADF} = \dfrac{1}{2}NO.AF + \dfrac{1}{2}DO .AF = \dfrac{DN.AF}{2}\)
Xét △NCM và △NAD, ta có:
∠AND = ∠CNM (góc đối đỉnh)
∠DAM = ∠DCM (Góc nội tiếp chắn cung DM của (O))
Suy ra △NCM ∽ △NAD ⇒ \(\dfrac{ND}{NM} = \dfrac{AD}{CM}\) ⇒ \({ND} = \dfrac{AD.NM}{CM}\) (*)
Tương tự △AFD ∽ △MFB ⇒ \(\dfrac{AF}{AD} = \dfrac{MF}{MB}\) ⇒ \({AF} = \dfrac{AD.MF}{MB}\) (**)
Xét △MCN và △MFB có:
\(\angle CMN = \dfrac{1}{2} \stackrel\frown{AC} = \dfrac{1}{2} \stackrel\frown{DB} = \angle FMB \)
\(\angle NCM = \dfrac{1}{2} \stackrel\frown{DM} = \dfrac{1}{2}(\stackrel\frown{DB}+\stackrel\frown{BM}) = \dfrac{1}{2}(\stackrel\frown{AD}+\stackrel\frown{BM})= \angle MFB \)
Suy ra △MCN ∽ △MFB ⇒ \(\dfrac{MC}{MN} = \dfrac{MF}{MB}\) ⇒ \(\dfrac{MN.MF}{MC.MB} = 1\) (***)
Nhân vế theo vế của (*) (**) và (***), ta có:
\({AF.ND}.\dfrac{MN.MF}{MC.MB} = \dfrac{{AD}^2.NM.MF}{CM.MB}.1\)
\(\Leftrightarrow {AF.ND} = {AD}^2\)
Hay \(S_{ANFD} = \dfrac{DN.AF}{2} = \dfrac{{AD}^2}{2} = const\)
Do giá trị \(AD = \sqrt 2 R\) không phụ thuộc vào M nên diện tích tứ giác ANFD không thay đổi theo M (đpcm)
Bài 5 (0,5 điểm). Cho x, y, z là các số dương thỏa mãn x + y + z= 2020.
Tìm giá trị lớn nhất của biểu thức:
\(P = \dfrac{xy}{\sqrt{2020z+xy}} + \dfrac{yz}{\sqrt{2020x+yz}}+ \dfrac{zx}{\sqrt{2020y+zx}}\)
\( = \dfrac{xy}{\sqrt{(x+y+z)z+xy}} + \dfrac{yz}{\sqrt{(x+y+z)x+yz}}+ \dfrac{zx}{\sqrt{(x+y+z)y+zx}}\)
\( = \dfrac{xy}{\sqrt{(y+z)(x+z)}} + \dfrac{yz}{\sqrt{(x+y)(x+z)}}+ \dfrac{zx}{\sqrt{(y+z)(y+x)}}\)
Áp dụng BĐT AM-GM cho cặp số \(\dfrac{xy}{{x+z}}\) và \(\dfrac{xy}{{y+z}}\), ta có:
\( \dfrac{xy}{\sqrt{(y+z)(x+z)}} \leq \dfrac{1}{2} \left( \dfrac{xy}{x+z} + \dfrac{xy}{y+z} \right)\)
\( \dfrac{yz}{\sqrt{(x+z)(x+y)}} \leq \dfrac{1}{2} \left( \dfrac{yz}{x+z} + \dfrac{yz}{x+y} \right)\)
\( \dfrac{zx}{\sqrt{(y+z)(y+x)}} \leq \dfrac{1}{2} \left( \dfrac{zx}{y+z} + \dfrac{zx}{x+y} \right)\)
Cộng vế theo vế 3 bất đẳng thức trên ta có:
\( \dfrac{xy}{\sqrt{(y+z)(x+z)}} + \dfrac{yz}{\sqrt{(x+y)(x+z)}}+ \dfrac{zx}{\sqrt{(y+z)(y+x)}} \leq \)
\(\dfrac{1}{2} \left( \dfrac{xy}{x+z} + \dfrac{xy}{y+z} +\dfrac{yz}{x+z} + \dfrac{yz}{x+y} + \dfrac{zx}{y+z} + \dfrac{zx}{x+y} \right)\)
\(\Leftrightarrow P \leq \dfrac{1}{2} \left( \dfrac{xy+yz}{x+z} + \dfrac{xy+zx}{y+z} + \dfrac{yz+x z}{x+y} \right) = \dfrac{1}{2} (y+x+z)=1010\)
Vậy \(max_P = 1010 \Leftrightarrow x=y=z= \dfrac{2020}{3}\).
-/-
Trên đây là đề thi thử vào 10 môn toán năm 2020 khảo sát chất lượng học sinh lớp 9 tại Quận Long Biên, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử vào lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
