Sở GD&ĐT tỉnh Tây Ninh vừa công bố đề thi thử tuyển sinh vào lớp 10 lần 1 môn Toán dành cho học sinh lớp 9 ôn luyện trong kỳ thi tuyển sinh vào lớp 10 năm học 2020/2021, dưới đây Đọc tài liệu xin gợi ý đáp án tham khảo cho đề thi này, các em cùng xem nhé:
Đề thi tham khảo
Đề thi minh họa vào lớp 10 môn Toán tỉnh Tây Ninh
Câu 1:(1,0 điểm)
Tính giá trị biểu thức \(S = \sqrt{36} – \sqrt{9} + \sqrt{16}\)
Câu 2:(1,0 điểm)
Tìm x để biểu thức \(T= \sqrt{3x-2}\) xác định.
Câu 3:(1,0 điểm)
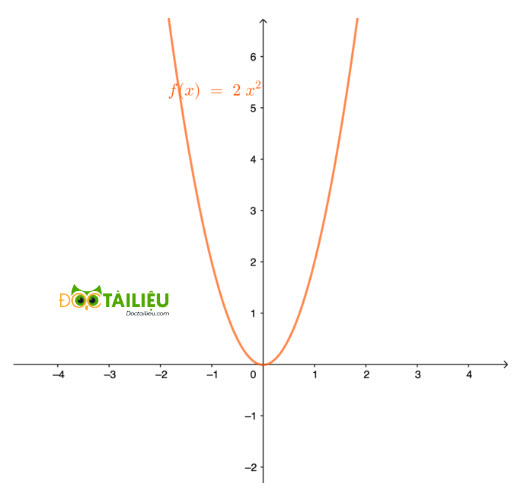
Vẽ đồ thị của hàm số y = 2x².
Câu 4:(1,0 điểm)
Tìm m để đường thẳng d: y = mx + 2m -3 đi qua điểm A(0;5).
Câu 5:(1,0 điểm)
Giải hệ phương trình
\(\left\{ \matrix{ 2x + y = 1 \hfill \cr 3x – 2y = 12 \hfill \cr} \right.\)
Câu 6:(1,0 điểm)
Cho hình thoi ABCD có AC = a, BD= 3a. Tính độ dài AB theo a.
Câu 7:(1,0 điểm)
Một mảnh vườn hình chữ nhật có chu vi bằng 28 m và độ dài đường chéo bằng 5/4 lần chiều dài của mảnh vườn đó. Tính diện tích của mảnh vườn đã cho.
Câu 8:(1,0 điểm)
Tìm a và b để đường thẳng d1: y = ax+b cắt đường thẳng d2, y = bx-a tại điểm M(2;1)
Câu 9:(1,0 điểm)
Cho tam giác ABC ( AC > AB) và ∠BAC = 60°. Trên cạnh AC lấy điểm D sao cho CD = AB. Gọi M, N lần lượt là trung điểm của AD và BC. Tính ∠CMN
Câu 10:(1,0 điểm)
Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của AB và AD, BN cắt CM tại P. Tính tỉ số giữa diện tích tam giác BMP và diện tích hình bình hành ABCD.
- Hết -
Trên đây là đề thi thử vào 10 môn Toán của tỉnh Tây Ninh năm 2020 do Sở ra đề, các em hãy thử làm bài trong 120 phút rồi tiến hành đối chiếu kết quả của mình nhé!
Đáp án đề thi thử Toán vào 10 Tây Ninh năm 2020
Câu 1:
\(S = \sqrt{36} – \sqrt{9} + \sqrt{16}\) \(=6-3+4 =7\)
Câu 2:
Để biểu thức \(T= \sqrt{3x-2}\) xác định
\(\Leftrightarrow 3x-2 \geq 0 \Leftrightarrow x\geq \dfrac{2}3\)
Câu 3:
Các em cần kẻ bảng tọa độ điểm rồi tiến hành vẽ:
Câu 4:
Để A thuộc (d) thì toạ độ điểm A phải thoả mãn phương trình (d):
\(5 = m.0 + 2m - 3\)
\(\Leftrightarrow m = 4\)
Câu 5:
\(\left\{ \matrix{ 2x + y = 1 \hfill \cr 3x – 2y = 12 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x=2 \hfill \cr y=-3 \hfill \cr} \right.\)
Câu 6:
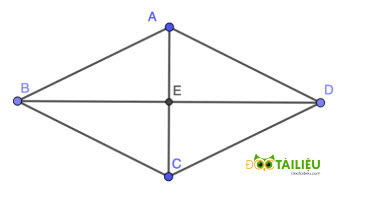
Gọi E là giao của AC và BD. Theo tính chất hình thoi ta có: AE = EC và DE = EB.
Áp dụng định lý Pytago cho △ABE vuông tại E, ta có:
\(AB = \sqrt{{AE}^2 + {EB}^2} = \sqrt{{\left(\dfrac{AC}2\right)}^2 + {\left(\dfrac{BD}2\right)}^2} \) \(=\sqrt{{\left(\dfrac{a}2\right)}^2 + {\left(\dfrac{3a}2\right)}^2} = \dfrac{a\sqrt{10}}2\)
Câu 7:
Gọi chiều dài và rộng của mảnh vườn đó lần lượt là A và B (mét, A,B > 0)
Độ dài đường chéo mảnh vườn là \(\sqrt{A^2+B^2}\) (m)
Theo bài ra ta có hệ:
\(\left\{ \matrix{ 2A+2B = 28 \hfill \cr \sqrt{A^2+B^2} = \dfrac{5}4 A \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr A^2 +B^2 = \dfrac{25}{16} A^2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr B^2 = \dfrac{9}{16} A^2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ A + B = 14 \hfill \cr B = \dfrac{3}{4} A \hfill \cr} \right.\) (vì A,B > 0)
\(\Leftrightarrow \left\{ \matrix{ A = 8 \hfill \cr B = 6 \hfill \cr} \right.\)
KL....
Câu 8:
Để d1 và d2 cắt nhau tại M(2;1) tức là toạ độ điểm M thoả mãn phương trình của d1 và d2:
\(\left\{ \matrix{ 1=2a+b \hfill \cr 1=2b-a \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ a = \dfrac{1}5 \hfill \cr b = \dfrac{3}5 \hfill \cr} \right.\)
Câu 9:
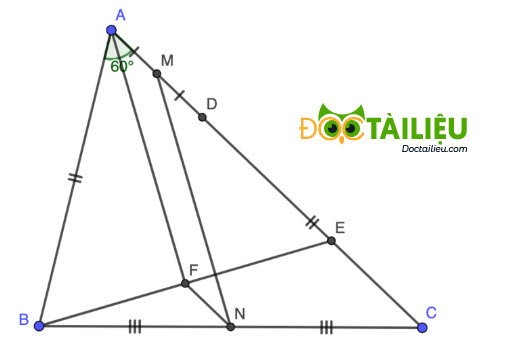
Trên AC lấy điểm E sao cho AE = AB = DC ⇒ AD + DE = DE + EC ⇒ AD = EC.
△AEB cân tại A, có ∠BAC = 60° ⇒ △AEB đều.
Lấy F là trung điểm BE, xét △CBE có F là trung điểm BE, N là trung điểm BC
⇒ FN là đường trung bình ⇒ FN // EC và \(FN = \dfrac{1}2 EC = \dfrac{1}2 AD = AM\)
Ta có FN // AM, FN = AM ⇒ AMNF là hình bình hành ⇒ MN // AF
Suy ra ∠CMN = ∠CAF = \(\dfrac{1}2 \angle BAC \) = 30°.
Câu 10:
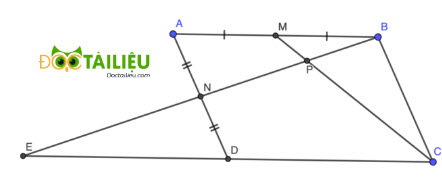
Vì M là trung điểm AB
⇒ \(MB = \dfrac{1}2 AB\) ⇒ \(S_{CMB} = \dfrac{1}2 S_{CAB} = \dfrac{1}4 S_{ABCD} \) (cùng độ dài chiều cao)
Kéo dài BN cắt CD tại E.
Dễ thấy EC = 2ED = 2DC.
Xét △PMB và △PCE, ta có:
∠EPC = ∠BPM (đối đỉnh)
∠PMB = ∠PCE (so le trong)
Suy ra △PMB ∽ △PCE ⇒ \(\dfrac{PM}{PC} = \dfrac{MB}{EC} = \dfrac{1}{4} \) ⇒ \(\dfrac{PM}{MC} = \dfrac{1}{5} \)
Suy ra \(MP = \dfrac{1}5 MC \)
⇒ \(S_{BMP} = \dfrac{1}5S_{BMC} = \dfrac{1}5 . \dfrac{1}4 S_{ABCD} = \dfrac{1}{20} S_{ABCD} \).
-/-
Trên đây là hướng dẫn giải đề thi tham khảo vào lớp 10 môn Văn năm 2020 tỉnh Tây Ninh mà Đọc tài liệu thực hiện, mong rằng các em sẽ ôn luyện thật tốt. Đừng quên còn rất nhiều tài kiệu đề thi thử tuyển sinh vào lớp 10 môn Toán của tất cả các trường và tỉnh thành trên cả nước đang đợi các em khám phá nhé.
