Đề thi khảo sát chất lượng môn Toán dành cho học sinh lớp 9 vào 10 của Quận Tây Hồ năm học 2020/2021 vừa công bố giúp các em học sinh lớp 9 thử sức và ôn luyện trước với cấu trúc đề thi, cùng Đọc tài liệu tham khảo đề thi và đáp án dưới đây nhé:
Đề thi thử Toán vào 10 năm 2020 quận Tây Hồ
PHÒNG GIÁO DỤC & ĐÀO TẠO QUẬN TÂY HỒ | ĐỂ KHẢO SÁT CHẤT LƯỢNG NĂM HỌC 2019 - 2020 Môn Toán lớp 9 – Thời gian: 90 phút |
Câu 1 (2,0 điểm).
a) Cho biểu thức A = \(\dfrac{x+7}{\sqrt{x}}\) với \(x > 0\). Tính giá trị của A khi \(x = 16\).
b) Cho biểu thức B = \(\dfrac{\sqrt{x}}{\sqrt{x}+3} + \dfrac{2\sqrt{x}-1}{\sqrt{x}-3} -\dfrac{1x-\sqrt{x}-3}{x-9} \)với \(x>0, x≠9\).
Rút gọn biểu thức B.
c) Tìm giá trị nhỏ nhất của biểu thức \(S = \dfrac{1}{B} +A \)
Câu 2 (2,0 điểm). Giải bài toán bằng cách phương trình hoặc hệ phương trình
Ngày thứ nhất hai tổ công nhân của một nhà máy sản xuất được 1500 chiếc khẩu trang. Để đáp ứng nhu cầu khẩu trang trong dịch cúm do chủng mới virus Corona gây ra nên ngày thứ hai tổ một vượt mức 35%, tổ hai vượt mức 40% so với ngày thứ nhất. Vì vậy hai tổ đã sản xuất được 2065 chiếc khẩu trang. Hỏi ngày thứ hai mỗi tổ sản xuất được bao nhiêu chiếc khẩu trang,
Câu 3 (2,5 điểm).
a) Giải phương trình: X⁴ - 8X² -9 = 0
b) Giải hệ phương trình: \(\left\{ \matrix{ x +\dfrac{1}{\sqrt{y-2}} = 3 \hfill \cr \dfrac{x}{2} + \dfrac{3}{\sqrt{y-2}} = -2 \hfill \cr} \right.\)
c) Khuê Văn Các là một lầu vuông tám mái, do Tổng trấn Nguyễn Văn Thành triều Nguyễn cho xây dựng vào năm 1805 trong Văn Miếu - Quốc Tử Giám ở Thăng Long, với tầng trên là kiến trúc gác gỗ sơn son thếp vàng hình lập phương ( trừ mái lợp). Biết thể tích của gác gỗ là 46,656 m², hãy tính độ dài cạnh gác gỗ của Khuê Văn Các.
Câu 4 (3,0 điểm). Cho đường tròn (O; R). Điểm M ở ngoài đường tròn sao cho OM = 2R. Kẻ hai tiếp tuyến MA, MB tới đường tròn (A; B là các tiếp điểm). Nối OM cắt AB tại H, Hạ HD⊥MA tại D. Điểm C thuộc cung nhỏ AB. Tiếp tuyến tại C của đường tròn (O; R) cắt MA, MB lần lượt tại E và F.
a) Chứng minh MAOB là tứ giác nội tiếp
b) Chứng minh OH.OM = OA²
c) Đường tròn đường kinh MB cắt BD tại I, gọi K là trung điểm OA. Chứng minh ba điểm M, I, K thẳng hàng.
Câu 5 (0,5 điểm). Giải phương trình:
\(x + \sqrt{17 - x^2} + x\sqrt{17 - x^2} = 9\)
Trên đây là mẫu đề thi khát sát chất lượng môn Toán lớp của Quận Tây Hồ năm 2020 vừa ra. Thử sức làm đề rồi tiến hành so sánh đối chiếu kết quả phía dưới nhé
Đáp án đề khát sát chất lượng môn Toán 9 Tây Hồ năm 2020
Câu 1 (2,0 điểm).
a) Cho biểu thức A = \(\dfrac{x+7}{\sqrt{x}}\) với \(x > 0\). Tính giá trị của A khi \(x = 16\).
Với \(x = 16\)\(\Rightarrow A=\frac{16+7}{\sqrt{16}}\)\(=\frac{23}{4}\).
b) Cho biểu thức B = \(\dfrac{\sqrt{x}}{\sqrt{x}+3} + \dfrac{2\sqrt{x}-1}{\sqrt{x}-3} -\dfrac{2x-\sqrt{x}-3}{x-9} \)với \(x>0, x≠9\).
Rút gọn biểu thức B.
Ta có:
\(B=\dfrac{\sqrt{x}}{\sqrt{x}+3} + \dfrac{2\sqrt{x}-1}{\sqrt{x}-3} -\dfrac{2x-\sqrt{x}-3}{x-9} \)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3} + \dfrac{2\sqrt{x}-1}{\sqrt{x}-3} -\dfrac{2x-\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)} \)
\(=\dfrac{\sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)} + \dfrac{(2\sqrt{x}-1)(\sqrt{x}+3)}{(\sqrt{x}-3)(\sqrt{x}+3)} -\dfrac{2x-\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)} \)
\(=\dfrac{\sqrt{x}(\sqrt{x}-3)+(2\sqrt{x}-1)(\sqrt{x}+3)-(2x-\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)} \)
\(=\dfrac{x-3\sqrt{x}+2x+5\sqrt{x}-3-2x+\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}+3)} \)
\(=\dfrac{x+3\sqrt{x}}{(\sqrt{x}-3)(\sqrt{x}+3)} \)
\(=\dfrac{\sqrt{x}(\sqrt{x}+3) }{(\sqrt{x}-3)(\sqrt{x}+3)} \)
\(=\dfrac{\sqrt{x} }{\sqrt{x}-3} \)
Vậy \(B=\dfrac{\sqrt{x} }{\sqrt{x}-3} \)
c) Tìm giá trị nhỏ nhất của biểu thức \(S = \dfrac{1}{B} +A \)
Ta có: \(S = \dfrac{1}{B} +A \) \(=\dfrac{\sqrt{x}-3}{\sqrt{x}}+\dfrac{x+7}{\sqrt{x}}\) \(=\dfrac{x+\sqrt{x}+4}{\sqrt{x}}\) \(=\sqrt{x}+\dfrac{4}{\sqrt{x}}+1\) \(=\big(\sqrt[4]{x}-\dfrac{2}{\sqrt[4]{x}}\big)^2+5\) \(\geq5\) với mọi \(x>0\)
Hay ta có \(Min \space S = 5 \Leftrightarrow \big(\sqrt[4]{x}-\dfrac{2}{\sqrt[4]{x}}\big)^2 = 0\) \(\Leftrightarrow \sqrt[4]{x}=\dfrac{2}{\sqrt[4]{x}}\) \(\Leftrightarrow \sqrt{x}=2\) \(\Leftrightarrow x=4\)
Câu 2 (2,0 điểm). Giải bài toán bằng cách phương trình hoặc hệ phương trình
Ngày thứ nhất hai tổ công nhân của một nhà máy sản xuất được 1500 chiếc khẩu trang. Để đáp ứng nhu cầu khẩu trang trong dịch cúm do chủng mới virus Corona gây ra nên ngày thứ hai tổ một vượt mức 35%, tổ hai vượt mức 40% so với ngày thứ nhất. Vì vậy hai tổ đã sản xuất được 2065 chiếc khẩu trang. Hỏi ngày thứ hai mỗi tổ sản xuất được bao nhiêu chiếc khẩu trang,
Gọi số khẩu trang mỗi tổ sản xuất được trong một ngày lần lượt là \(K_1\) và \(K_2\). Theo giả thiết đề bài ta có:
\(\left\{ \matrix{ K_1+K_2=1500 \hfill \cr 1,35K_1+1,4K_2=2065 \hfill \cr} \right. \)
Giải hệ trên ta có \(\left\{ \matrix{ K_1= 700 \hfill \cr K_2=800 \hfill \cr} \right. \)
Suy ra ngày thứ hai mỗi tổ sản xuất được:
Tổ 1 \(=1,35K_1=945\) (khẩu trang)
Tổ 2 \(=1,4K_2=1120\) (khẩu trang)
Câu 3 (2,5 điểm).
a) Giải phương trình: \(x^4-8x^2-9=0\)
Ta có:
\(x^4-8x^2-9=0\)
\(\Leftrightarrow (x^2-9)(x^2+1)=0\)
\(\Leftrightarrow x^2-9=0\) (vì \(x^2 +1 \geq1 >0\))
\(\left[ \matrix{ {x} = {3} \hfill \cr {x} = {-3} \hfill \cr} \right.\)
Vậy phương trình đã cho có 2 nghiệm là \(x = \{3;-3\}\)
b) Giải hệ phương trình: \(\left\{ \matrix{ x +\dfrac{1}{\sqrt{y-2}} = 3 \hfill \cr \dfrac{x}{2} + \dfrac{3}{\sqrt{y-2}} = -2 \hfill \cr} \right.\)
ĐKXĐ: \(y>2\)
\(\Leftrightarrow \left\{ \matrix{ 3x +\dfrac{3}{\sqrt{y-2}} =9 \hfill \cr \dfrac{x}{2} + \dfrac{3}{\sqrt{y-2}} = -2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ 3x +\dfrac{3}{\sqrt{y-2}} =9 \hfill \cr \dfrac{5x}{2} =11 \hfill \cr} \right.\) (trừ vế theo vế phương trình 1 cho 2)
\(\Leftrightarrow \left\{ \matrix{ x +\dfrac{1}{\sqrt{y-2}} =3 \hfill \cr x=\dfrac{22}{5} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ \dfrac{1}{\sqrt{y-2}} =3-x=3-\dfrac{22}{5}=\dfrac{-7}{5} \hfill \cr x=\dfrac{22}{5} \hfill \cr} \right.\)
Vô nghiệm vì \(\dfrac{1}{\sqrt{y-2}} >0 \) với mọi y.
c) Khuê Văn Các là một lầu vuông tám mái, do Tổng trấn Nguyễn Văn Thành triều Nguyễn cho xây dựng vào năm 1805 trong Văn Miếu - Quốc Tử Giám ở Thăng Long, với tầng trên là kiến trúc gác gỗ sơn son thếp vàng hình lập phương ( trừ mái lợp). Biết thể tích của gác gỗ là 46,656 m², hãy tính độ dài cạnh gác gỗ của Khuê Văn Các.
Gọi độ dài cạnh gác gỗ là x (m²)
Ta có \(x^3=46,656\) (m³)
\(\Leftrightarrow x = 3,6\) (m)
Vậy độ dài cạnh gác gỗ của Khuê Văn Các là 3,6 m
Câu 4 (3,0 điểm). Cho đường tròn (O; R). Điểm M ở ngoài đường tròn sao cho OM = 2R. Kẻ hai tiếp tuyến MA, MB tới đường tròn (A; B là các tiếp điểm). Nối OM cắt AB tại H, Hạ HD⊥MA tại D. Điểm C thuộc cung nhỏ AB. Tiếp tuyến tại C của đường tròn (O; R) cắt MA, MB lần lượt tại E và F.
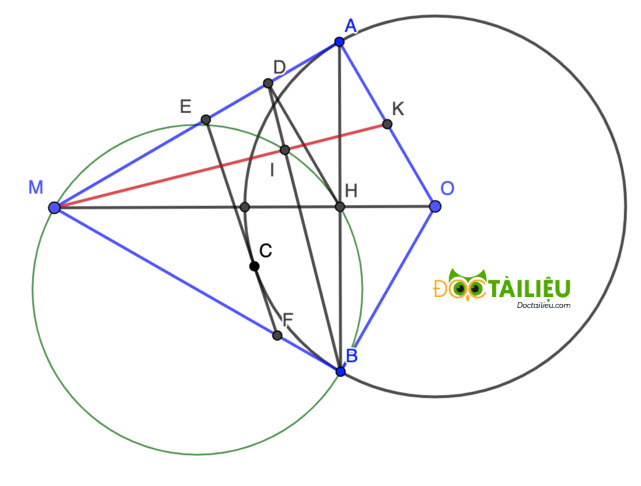
a) Chứng minh MAOB là tứ giác nội tiếp
Vì MA, MB lần lượt là tiếp tuyến với (O,R), mà A và B là các tiếp điểm \(\Leftrightarrow \left\{ \matrix{ MA⊥OA \hfill \cr MB⊥OB \hfill \cr} \right.\) hay \(\angle MAO = \angle MBO = 90⁰\)
\(\Rightarrow\) Tứ giác MAOB là tứ giác nội tiếp (đpcm)
b) Chứng minh OH.OM = OA²
Dễ thấy \(OM ⊥ AB\) (tính chất dây cung) hay \(\angle AHO= 90⁰\)
Xét tam giác AHO và MAO, ta có:
\(\left\{ \matrix{ \angle AOM \space chung \hfill \cr \angle AHO=\angle MAO = 90⁰ \hfill \cr} \right.\) \(\Rightarrow \triangle AHO ∽ \triangle MAO\)
\(\Rightarrow \frac{OA}{OH}=\frac{OM}{OA}\)\(\Leftrightarrow OH.OM = OA^2\) (đpcm)
c) Đường tròn đường kinh MB cắt BD tại I, gọi K là trung điểm OA. Chứng minh ba điểm M, I, K thẳng hàng.
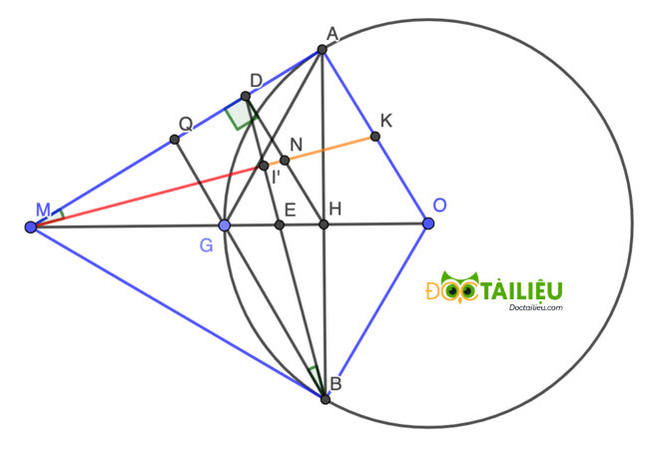
Gọi MK cắt BD tại I', cắt DH tại N. G là giao điểm của (O,R) cắt MO, theo giả thiết ta có MO = 2R = 2.OG \(\Rightarrow\) G là trung điểm OM.
Xét tam giác OMA vuông tại A, có OM = 2R = 2.OA \(\Rightarrow\) \(\angle AOM = 60⁰\) và \(\angle AMO = 30⁰\) .
Tam giác OAG cân tại O (do OG và OA cùng là bán kính của đường tròn O) có \(\angle AOM = 60⁰\) \(\Rightarrow\) tam giác OAG đều, hay tam giác OBG cũng đều.
Lại có AH ⊥ OG (chứng minh phần trên) \(\Rightarrow\) AH đồng thời là đường cao cũng là trung tuyến của tam giác đều OAG hay H là trung điểm GO.
Chứng minh được tam giác MAB cân tại M (chứng minh phần trên), có \(\angle AMO = \angle OMB = 30⁰\) hay \(\angle AMB = 60⁰\) hay tam giác AMB đều.
Ta đã có: H là trung điểm GO \(\Rightarrow\) \(HG = \frac{1}{2}GO = \frac{1}{2}MG\) \(\Rightarrow\) G là trực tâm tam giác đều AMB \(\Rightarrow\) BG ⊥ MA.
Xét 2 tam giác MAO và BQA, có \(\left\{ \matrix{ \angle AQB = \angle MAO = 90⁰ \hfill \cr \angle BAQ = \angle MOA = 60⁰ \hfill \cr} \right.\) \(\Rightarrow\) \(\triangle MAO ∽ \triangle BQA\) (g.g)
\(\Rightarrow\) \(\frac{AM}{BQ} = \frac{AO}{AQ}\)
Xét hình thang GQAO (GQ // AO do cùng ⊥ AM), có H là trung điểm GO (chứng minh trên), HD // AO (do cùng ⊥ AM) \(\Rightarrow\) HD là đường trung bình của hình thang GQAO hay D là trung điểm AQ.
\(\frac{QD}{QA} = \frac{1}{2} = \frac{AK}{AO}\) \(\Rightarrow\) \(\frac{AO}{AQ} = \frac{AK}{QD} = \frac{AM}{BQ} \) (từ chứng minh trên)
Xét 2 tam giác MAK và BQD, có \(\left\{ \matrix{ \angle AQB = \angle MAO = 90⁰ \hfill \cr \frac{AK}{QD} = \frac{AM}{BQ} \hfill \cr} \right.\) \(\Rightarrow\) \(\triangle MAO ∽ \triangle BQA\) (c.g.c)
\(\Rightarrow\) \(\angle QBD = \angle AMK\)
Lại có \(\angle AMO = \angle ABQ = 30⁰\) Suy ra \(\angle AMO - \angle AMK = \angle ABQ - \angle QBD\) \(\Leftrightarrow\) \(\angle DBA = \angle KMO\)
Gọi BD cắt OM tại E. Xét 2 tam giác MI'E và BHE, có \(\left\{ \matrix{ \angle MEI' = \angle BEH \space (đối \space đỉnh) \hfill \cr \angle HBE =\angle DBA = \angle KMO = \angle I'ME \hfill \cr} \right.\) \(\Rightarrow\) \(\triangle MI'E ∽ \triangle BHE\) (g.g) \(\Rightarrow\) \(\angle MI'E = \angle BHE = \angle BHM = 90⁰\) \(\Rightarrow\) MI' ⊥ DB hay MK ⊥ DB tại I'. (1)
Ta lại có DB cắt đường tròn đường kính MB tại điểm thứ hai là I \(\Rightarrow\) \(\angle MIB = 90⁰\) \(\Leftrightarrow\) MI ⊥ DB (2)
Từ (1) và (2) suy ra I và I' trùng nhau, hay I nằm trên MK, tức là M I K thẳng hàng (đpcm)
Câu 5 (0,5 điểm). Giải phương trình:
\(x + \sqrt{17 - x^2} + x\sqrt{17 - x^2} = 9\) (1)
ĐKXĐ \(x^2 \leq 17 \Leftrightarrow -\sqrt{17} \leq x \leq \sqrt{17}\)
Đặt \(\sqrt{17 - x^2} = y\) (ĐK \(y\geq 0\))
Ta có: \(\sqrt{17 - x^2} = y\) \(\Leftrightarrow y^2 = 17 - x^2\) \(\Leftrightarrow x^2+y^2 = 17 \) (2)
Thay y vào (1) ta có:
(1) \(\Leftrightarrow x+y+xy = 9\)
Kết hợp (1) và (2) ta có hệ: \(\left\{ \matrix{ x^2+y^2 = 17 \hfill \cr x+y+xy = 9 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{(x+y)^2 - 2xy = 17 \hfill \cr xy = 9-(x+y) \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{(x+y)^2 - 2[9 - (x+y)] = 17 \hfill \cr xy = 9-(x+y) \hfill \cr} \right.\) (thay xy từ phương trình dưới lên)
\(\Leftrightarrow \left\{ \matrix{(x+y)^2 + 2(x+y) - 35=0 \hfill \cr xy = 9-(x+y) \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{(x+y-5)(x+y+7)=0 \hfill \cr xy = 9-(x+y) \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ \left\{ \matrix{x+y=5 \hfill \cr xy = 9-(x+y) \hfill \cr} \right. \hfill \cr \left\{ \matrix{x+y=-7 \hfill \cr xy = 9-(x+y) \hfill \cr} \right. \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ \left\{ \matrix{x+y=5 \hfill \cr xy = 4 \hfill \cr} \right. \hfill \cr \left\{ \matrix{x+y=-7 \hfill \cr xy = 16 \hfill \cr} \right. \hfill \cr} \right.\)
TH 1: \(\left\{ \matrix{x+y=5 \hfill \cr xy = 4 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{y = 5 - x \hfill \cr x(5-x) = 4 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{y = 5 - x \hfill \cr x^2-5x+4=0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{y = 5 - x \hfill \cr \left[ \matrix{ {x} = {-1} \hfill \cr {x} = {-4} \hfill \cr} \right.\hfill \cr} \right.\) \(\Leftrightarrow \left[ \matrix{ (x;y) = (-1;6) \hfill \cr (x;y) = (-4;9) \hfill \cr} \right.\) (cả 2 nghiệm đều thỏa mãn đkxđ)
TH 2: \(\left\{ \matrix{x+y=-7 \hfill \cr xy = 16 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{y = -7 - x \hfill \cr x(-7-x) = 16 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{y = -7 - x \hfill \cr x^2+7x+16=0 \hfill \cr} \right.\)
Vô nghiệm.
Vậy phương trình đã cho có 2 nghiệm \(x=-1\) hoặc \(x=-4\)
-/-
Trên đây là hướng dẫn đề thi khảo sát chất lượng cho học sinh lớp 9 vào lớp 10 môn toán năm 2020 của Quận Tây Hồ, mong rằng đây sẽ là tài liệu hữu ích giúp các em ôn tập. Đừng quên còn rất nhiều tài liêu đề thi thử lớp 10 môn toán khác của các tỉnh thành trên cả nước nhé.
