Sở GD&ĐT Vĩnh Long vừa công bố đề thi tuyển sinh vào lớp 10 tham khảo năm học 2020/2021 môn Toán như sau:
Đề thi tham khảo
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT VĨNH LONG
NĂM HỌC 2020 – 2021
Môn thi: TOÁN ĐỀ THAM KHẢO
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1. (1.0 điểm)
Tính giá trị biểu thức
a) \(A = \sqrt {25} + 3\sqrt 8 - 2\sqrt {18} \)
b) \(B = \sqrt {\frac{1}{2}} + \frac{{\sqrt 5 - 1}}{{\sqrt {10} - \sqrt 2 }} - \sqrt {3 - 2\sqrt 2 } \)
Bài 2. (2.0 điểm)
Giải các phương trình và hệ phương trình sau:
a) \(x^2 + x - 20 = 0\)
b) \(\frac{{x + 2}}{2} - 1 = 0\)
c) \({(x - 1)^4} - 8{(x - 1)^2} - 9 = 0\)
d) \( \left\{ \matrix{ 2x - y = -7 \hfill \cr 3x + y = 27 \hfill \cr} \right.\)
Bài 3. (2.0 điểm)
a) Cho hàm số \(y = 2x-1\) có đồ thị là đường thẳng (d) và hàm số \(y =x^2\) có đồ thị là parabol (P). Vẽ đường thẳng (d) và tìm tọa độ giao điểm của parabol (P) và đường thẳng (d) bằng phép tính.
b) Cho phương trình \(x^2 -2 (m+1) x + 6m - 4 =0\) (1) (với m là tham số). Tìm m để phương trình (1) có hai nghiệm \(x_1, x_2\) thỏa mãn \((2m - 2)x_1+x_2^2-4x_2=4\)
Bài 4. (1.0 điểm).
Hai thành phố A và B cách nhau 150km. Một xe máy khởi hành từ A đến B, cùng lúc đó một ôtô cũng khởi hành từ B đến A với vận tốc lớn hơn vận tốc của xe máy là 10 km/h. Ôtô đến 4 được 30 phút thì xe máy cũng đến B. Tính vận tốc của mỗi xe.
Bài 5. (1.0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4 cm , CH = 9 cm. Tính độ dài đường cao AH và số đo ∠ABC (số đo góc làm tròn đến độ).
Bài 6. (2.5 điểm)
Cho đường tròn tâm O và điểm P nằm ngoài (O). Vẽ tiếp tuyến PC của (O) (C là tiếp điểm) và cát tuyến PAB (PA & PB) sao cho các điểm A, B, C nằm củng phía so với đường thẳng PO. Gọi M là trung điểm của đoạn thẳng AB và CD là đường kính cun (0)
a) Chứng minh tứ giác PCMO nội tiếp được đường tròn.
b) Gọi E là giao điểm của hai đường thẳng PO và BD. Chứng minh AM.DE = AC.DO.
c) Chứng minh CE vuông góc với CA
Bài 7. (0.5 điểm)
Chứng minh rằng \({x_0} = \sqrt[3]{{9 + 4\sqrt 5 }} + \sqrt[3]{{9 - 4\sqrt 5 }}\) là một nghiệm của phương trình sau \({({x^3} - 3x - 17)^{2020}}-1=0\)
HẾT
Đáp án đề tham khảo vào 10 môn Toán tỉnh Vĩnh Long năm 2020
Bài 1.
a) \(A = \sqrt {25} + 3\sqrt {8} - 2\sqrt {18} = 5 + 6\sqrt {2} - 6\sqrt {2} = 5\)
KL: ...
b) \(B = \sqrt {\frac{1}{2}} + \frac{{\sqrt 5 - 1}}{{\sqrt {10} - \sqrt 2 }} - \sqrt {3 - 2\sqrt 2 } \)
\(B = {\frac{1}{\sqrt2}} + {\frac{1}{\sqrt2}} - \sqrt {(\sqrt 2-1)^2} \)
\(B = \sqrt2 - \sqrt 2-1\)
\(B = -1\)
KL: ...
Bài 2.
a) \(x^2 + x - 20 = 0\)
⇔ \(x^2 + 5x - 4x- 20 = 0\)
⇔\((x+5)(x-4)=0\)
⇔\(\left[ \begin{align}& x+5=0 \\& x-4=0 \\\end{align} \right.\\\)
⇔\(\left[ \begin{align}& x=-5 \\& x=4 \\\end{align} \right.\\\)
KL: ...
b) \(\frac{{x + 2}}{2} - 1 = 0\)
⇔ x = 0
KL: ...
c) \({(x - 1)^4} - 8{(x - 1)^2} - 9 = 0\)
d) \( \left\{ \matrix{ 2x - y = -7 \hfill \cr 3x + y = 27 \hfill \cr} \right.\)
⇔\( \left\{ \matrix{ 5x =20 \hfill \cr 3x + y = 27 \hfill \cr} \right.\)
⇔\( \left\{ \matrix{ 5x =20 \hfill \cr 3x + y = 27 \hfill \cr} \right.\)
⇔ \(\left\{ \matrix{ x = 4 \hfill \cr y = 15 \hfill \cr} \right.\)
KL: ...
Bài 3. (2.0 điểm)
a) Vẽ d: y = 2x-1, (P): y = \(x^2\)
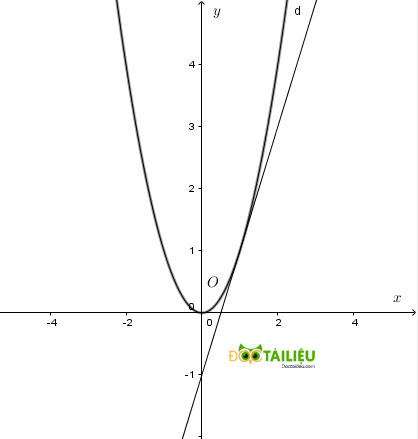
Tọa độ giao điểm của parabol (P) và đường thẳng (d) là nghiệm của phương trình
\(x^2 = 2x-1\) ⇔ \(x^2 - 2x+1=0\)
⇔ \((x-1)^2=0\)
⇔ \(x=1\) => y = 1.
KL: ...
ương trình \(x^2 -2 (m+1) x + 6m - 4 =0\) (1) có hai nghiệm\(x_1, x_2\) khi và chỉ khi
\(△'=(m+1)^2-(6m-4)>0\)
⇔\(△'=m^2-4m+5=(m-2)^2+1>0\,\,\,∀m\)
Theo định lý Viet ta có
\(\left\{ \matrix{ x_1+x_2=2(m+1) \hfill \cr x_1x_2 = 6m-4 \hfill \cr} \right.\)(*)
Lại có \(x_2\) là nghiệm của (1) => \(x_2^2 -2 (m+1) x_2 + 6m - 4 =0\)
⇔\(x_2^2 -2mx_2 -2x_2 + 6m - 4 =0\)
⇔\(x_2^2 -4x_2 - 4-2mx_2 +2x_2 + 6m =0\)
⇔\(x_2^2 -4x_2 - 4=2mx_2 -2x_2 - 6m\) (**)
Vì \(x_1, x_2\) bài cho thỏa mãn \((2m - 2)x_1+x_2^2-4x_2=4\)
⇔\((2m - 2)x_1+x_2^2-4x_2-4=0\)
Thế (**) vào ta có phương trình
\((2m - 2)x_1+2mx_2-2x_2-6m=0\)
⇔\((2m - 2)(x_1+x_2)-6m=0\)
Thế tiếp (*) vào ta có phương trình
\((2m - 2)(2(m+1))-6m=0\)
⇔\(4m^2 - 4 - 6m = 0\)
⇔\(4m^2 - 8m + 2m - 4 = 0\)
⇔ \((4m+2)(m-2)=0\)
⇔\(\left[ \begin{align}& m=2 \\& m= \dfrac{-1}{2}\\\end{align} \right.\\\)(t/m)
KL: ...
Bài 4.
Gọi vận tốc của xe máy là x (km/h), vận tốc của ô tô là y (km/h) (Điều kiện \(x, y >10\))
Đổi 30 phút = \(\dfrac{1}{2}\) giờ
Theo bài ta sẽ có hệ phương trình
\(\left\{ \matrix{ y = x + 10 \hfill \cr \dfrac{150}{x} - \dfrac{150}{y} = \dfrac{1}{2} \hfill \cr} \right.\)
Ta giải được nghiệm như sau \(\left\{ \matrix{ x = 50 \hfill \cr y = 60 \hfill \cr} \right. \)
KL: ...
Bài 5.
Ta có hình vẽ
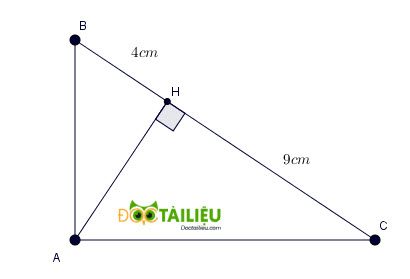
Theo định lý Pytago ta dễ dàng tính được AH:
HA² + HB ² + HC² + HA² = AB² + AC² = BC²
=> AH = 6
=> \(tan∠ABC = \dfrac{AH}{BH} = \dfrac{6}{4} = \dfrac{3}{2}\)
=> ∠ABC = 56,31⁰
Bài 6. (2.5 điểm)
a,
Vì PC là tiếp tuyến của (O) tại C nên PC ⊥ OC \(\Leftrightarrow \angle PCO = 90 ⁰\)
M là trung điểm AB \(\Rightarrow OM ⊥ AB \Leftrightarrow \angle OMA = 90 ⁰\)
Tứ giác PCMO có \(\angle PCO = \angle OMA = 90 ⁰\)\(\Rightarrow\) Tứ giác PCMO nội tiếp (đpcm)
b,
Vì tứ giác PCMO nội tiếp \(\Rightarrow\) \(\angle PMC = \angle POC \) (góc nội tiếp chắn cung PC) \(\angle DOE\) (góc đối đỉnh O) hay \(\angle AMC = \angle DOE \)
Xét \(\triangle AMC \) và \(\triangle DOE \), ta có:
\(\angle AMC = \angle DOE \)
\(\angle CAM = \angle ODE \) (góc nội tiếp (O) cùng chắn cung CB)
\(\Rightarrow\) \(\triangle AMC ∽ \triangle DOE\) \(\Rightarrow\) \(\frac{AM}{AC}=\frac{DO}{DE}\) \(\Leftrightarrow AM.DE = AC.DO\) (đpcm)
c,
Từ ý b, ta có \(\triangle AMC ∽ \triangle DOE\) \(\Rightarrow\) \(\frac{CM}{OE}=\frac{AM}{DO}\)
Mà AM = MB (do M là trung điểm AB), OD = OC = r (cùng là bán kính của (O))
nên \(\frac{CM}{OE}=\frac{BM}{OC}\)
Lại có \(\angle AMC = \angle DOE \) \(\Leftrightarrow\) \(180⁰ - \angle CMB = 180⁰ -\angle COE \) \(\Leftrightarrow\) \(\angle CMB = \angle COE \)
Từ 2 điều trên \(\Rightarrow\) \(\triangle COE ∽ \triangle BMC\) \(\Rightarrow\) \(\angle OCE = \angle MBC \)
\(=\angle CDA \) (góc nội tiếp (O) cùng chắn cung AC) hay \(\angle OCE = \angle CDA \), mà 2 góc này nằm ở vị trí so le trong tạo bởi đường thẳng DC cắt AD và CE \(\Rightarrow\) AD // CE
Mà AD ⊥ AC => AC ⊥ EC (đpcm)
Bài 7. (0.5 điểm)
Đặt \(a = \sqrt[3]{{9 + 4\sqrt 5 }}\) và \(b=\sqrt[3]{{9 - 4\sqrt 5 }}\), ta có: \({x_0} =a+b \)
Ta có: \(ab = \sqrt[3]{{9 + 4\sqrt 5 }} . \sqrt[3]{{9 - 4\sqrt 5}} \)\(= \sqrt[3]{({9 + 4\sqrt 5 })({9 - 4\sqrt 5})} \)\( =1\)
Xét Biểu thức \(M = {x_0^3} - 3x_0 - 18\)
\(={(a+b)^3} - 3(a+b) - 18\)
\(=a^3+b^3 + 3ab(a+b) - 3(a+b) - 18 \)
\(=a^3+b^3 + 3(a+b) - 3(a+b) - 18\) (vì \(ab=1\))
\(=a^3+b^3 - 18\)
\(=(9+4\sqrt5) +(9-4\sqrt5) - 18=0\)
Hay \(x_0\) là 1 nghiệm của phương trình \(x^3 - 3x - 18 = 0\) (1)
Ta có \({({x^3} - 3x - 17)^{2020}}-1=0\) có 1 nghiệm thoả mãn \(x^3 - 3x - 17=1\)
\(\Leftrightarrow x^3 - 3x - 18 = 0\) (2)
Từ (1) và (2) \(\Rightarrow \) \(x_0\) là 1 nghiệm của phương trình \({({x^3} - 3x - 17)^{2020}}-1=0\) (đpcm)
Trên đây là đáp án đề thi tham khảo tuyển sinh môn Toán vào 10 Vĩnh Long năm 2020, mong rằng với nội dung này các em sẽ thử sức đề thi thử vào lớp 10 2020 môn toán và ôn luyện kiến thức thật tốt!