Vừa qua thì các em học sinh lớp 9 tại huyện Phú Mỹ đã thực hiện bài thi kiểm tra cuối học kì 2 của mình đối với môn Toán, đây là một tài liệu khá hay mà Đọc tài liệu muốn gửi tới các em tham khảo để chuẩn bị tốt hơn cho kì thi vào 10 sắp tới:
Đề thi
Phần I. Trắc nghiệm khách quan (4,0 điểm)
Chọn và ghi vào bài làm chỉ một chữ cái in hoa đứng trước câu trả lời đúng nhất.
Câu 1: Cho phương trình x - 2y = 2 (1), phương trình nào trong các phương trình sau kết hợp với (1) được một hệ phương trình có nghiệm duy nhất ?
A. \(-\dfrac{1}2x + y = -1\)
B. \(\dfrac{1}2x - y = -1\)
C. \(2x-3y=3\)
D. \(2x-4y=4\)
Câu 2: Toạ độ giao điểm M của hai đường thẳng (d1): 5x - 2y - 3 = 0 và (d2): x + 3y - 4 = 0 là:
A. M(1;2)
B. M(1;-1)
C. M(1;1)
D. M(2;1)
Câu 3: Với giá trị nào của a và b thì hệ phương trình \(\left\{ \matrix{ ax + 2y = 1 \hfill \cr 3x - by = -2 \hfill \cr} \right.\)
có nghiệm (x; y) = (2;-1)A. \(a = \dfrac{1}2;b =-4\)
B. \(a = \dfrac{3}2;b =8\)
C. \(a = \dfrac{3}2;b =-8\)
D. \(a = \dfrac{1}2;b =4\)
Câu 4: Cho hàm số \(y = f(x)=\dfrac{1}5x^2\). Phát biểu nào sau đây là sai ?
A. Hàm số xác định với mọi số thực x, có hệ số \(a=\dfrac{1}5\)
B. Hàm sổ đồng biến khi \(x và nghịch biến khi \(x > 0\)
C. f(0) = 0; f(5) = 5; f(-5) = 5; f(-a) = f(a)
D. Nếu f(x) = 0 thì x = 0 và nếu f(x) = 1 thì \(x=±\sqrt{5}\)
Câu 5: Phương trình \((m + 1)x^2 - 2mx + 1 = 0\) là phương trình bậc hai khi:
A. m = 1.
B. m ≠ 1.
C. m = 0.
D. mọi giá trị của m.
Câu 6:
Hai phương trình: \(x^2 + ax + 1 = 0\) và \(x^2 – x – a = 0\) có một nghiệm thực chung khi a bằng:A. 0
B. 1
C. 2
D. 3
Câu 7: Cho phương trình \(0,1x^2 – 0,6x – 0,8 = 0\), với \(x_1;x_2\) là nghiệm của phương trình. Khi đó:
A. \(x_1 + x_2 = 0,6; x_1 x_2 = 8\)
B. \(x_1 + x_2 = 6; x_1 x_2 = 0,8\)
C. \(x_1 + x_2 = 6; x_1 x_2 = 8\)
D. \(x_1 + x_2 = 6; x_1 x_2 =- 8\)
Câu 8: Toạ độ giao điểm của (P) \(y=x^2\) và đường thẳng (d) y = 2x là:
A. O(0;0) và N(0;2)
B. O(0;0) và N(2;4)
C. M(0;2) và H(0;4)
D, M(2;0) và H(0;4)
Câu 9: Hình tam giác cân có cạnh đáy bằng 8cm, góc đáy bằng 30°. Khi đó độ dài đường tròn ngoại tiếp tam giác ABC bằng:
A. \(8 \pi \sqrt 3\)
B. \(\dfrac {16 \pi \sqrt 3}{3}\)
C. \(16 \pi \sqrt 3\)
D. \(\dfrac {8\pi \sqrt 3}{3}\)
Câu 10: Tứ giác nào sau đây nội tiếp được đường tròn ?
A. Hình bình hành.
B. Hình thoi.
C. Hình chữ nhật.
D. Hình thang.
Câu 11: Diện tích hình quạt tròn cung 60° của đường tròn có bán kính bằng 2 cm là:
A. \(\dfrac{2 \pi}{3} \space {cm}^2\)
B. \(\dfrac{2}{3 \pi} \space {cm}^2\)
C. \(\dfrac{ \pi}{3} \space {cm}^2\)
D. \(\dfrac{ 3}{\pi} \space {cm}^2\)
Câu 12: Bán kính của một đường tròn nội tiếp tam giác có ba cạnh lần lượt bằng 3cm. 4cm và 5cm là:
A, 1 cm
B. 1,5 cm
C. 2 cm
D. 2,5 cm
Câu 13: Độ dài cung tròn 120° của đường tròn có bán kính 3 cm là:
A. \(\pi \space cm\)
B. \(2\pi \space cm\)
C. \(3\pi \space cm\)
D. Kết quả khác
Câu 14: Thể tích một hình cầu bằng \(972 \pi\space {cm}^3\). Bán kính hình cầu bằng:
A. 9 cm
B. 18 cm
C. 27 cm
D. 36 cm
Câu 15: Một hình trụ có diện tích xung quanh bằng \(128 \pi\space {cm}^2\), chiều cao bằng bán kính đáy. Khi đó thể tích của nó bằng:
A. \(64 \pi\space {cm}^3\)
B. \(128\pi\space {cm}^3\)
C. \(34 \pi\space {cm}^3\)
D. \(512 \pi\space {cm}^3\)
Câu 16: Một hình nón có bán kính đáy là 5cm, chiều cao bằng 12cm. Khi đó diện tích xung quanh bằng:
A. \(60 \pi\space {cm}^2\)
B. \(300 \pi\space {cm}^2\)
C. \(17 \pi\space {cm}^2\)
D. \(65 \pi\space {cm}^2\)
Phần II. Tự luận: (6,0 điểm)
Câu 17: (1,0 điểm) Giải các phương trình và hệ phương trình sau:
a/ \(2x^4-3x^2-2=0\)
b/ \(\left\{ \matrix{ 4x - 5y = -13 \hfill \cr 5x -2 y = 5 \hfill \cr} \right. \)
Câu 18: (2,0 điểm)
a/ Cho phương trình \( x^2 – 4x + m =0 \) (m là tham số). Tìm m để phương trình có hai nghiệm x1, x2 thỏa mãn điều kiện: \(\dfrac{1}{x_1^2} + \dfrac{1}{x_2^2} = 2\)
b/ Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Tìm một số tự nhiên có hai chữ số, biết rằng chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 và nếu đổi chỗ hai chữ số cho nhau thì được số mới bằng \(\dfrac{4}{7}\) số ban đầu.
Câu 19: (2,5 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Tiếp tuyển tại A của (O; R) cắt tia CB tại điểm M.
a) Chứng minh MA² = MB.MC
b) Gọi H là chân đường cao hạ từ A xuống BC. Chứng minh AB.AC = 2R.AH.
c) Trên cạnh BC lấy điểm N tùy ý (N khác B và C). Gọi E, F lần lượt là hình chiếu vuông góc của N lên AB, AC. Tìm vị trí của N để độ dài đoạn EF nhỏ nhất.
Câu 20: (0,5 điểm) Cho phương trình: \(x^4-16x^2+32 = 0\) (với x ∈ ℝ)
Chứng minh rằng \(x = \sqrt{6 - 3 \sqrt{2+ \sqrt 3}} - \sqrt{2 + \sqrt{2+ \sqrt 3}}\)là một nghiệm của phương trình đã cho.
Hết
Đừng quên còn rất nhiều tài liệu đề thi thử vào lớp 10 môn Toán khác của các tỉnh thành trên cả nước đợi em khám phá nhé!
Đáp án đề kiểm tra học kì 2 huyện Phú Mỹ 2020
Phần I: Trắc nghiệm khách quan
| Câu 1 | C | Câu 9 | B |
| Câu 2 | C | Câu 10 | C |
| Câu 3 | C | Câu 11 | A |
| Câu 4 | B | Câu 12 | D |
| Câu 5 | B | Câu 13 | B |
| Câu 6 | B | Câu 14 | A |
| Câu 7 | D | Câu 15 | D |
| Câu 8 | B | Câu 16 | D |
Phần II: Tự luận
Câu 17: (1,0 điểm)
a/ \(2x^4-3x^2-2=0\)
\(\Leftrightarrow (2x^2+1)(x^2 - 2) = 0\)
\(\Leftrightarrow x^2 = 2\) (do \(2x^2+1 \geq 1 > 0\) với mọi x)
\(\Leftrightarrow x= ±\sqrt 2\)
b/ \(\left\{ \matrix{ 4x - 5y = -13 \hfill \cr 5x -2 y = 5 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{ x=3 \hfill \cr y=5 \hfill \cr} \right.\)
Câu 18: (2,0 điểm)
a/
Phương trình có hai nghiệm khi:
\(\Delta' = 2^2 - m = 4-m \geq 0\) \(\Leftrightarrow m \leq 4\)
Áp dụng hệ thức Vi-ét cho phương trình, ta có:
\(\left\{ \matrix{ x_1+x_2 = 4 \hfill \cr x_1x_2 = m \hfill \cr} \right.\)
Ta có: \(\dfrac{1}{x_1^2} + \dfrac{1}{x_2^2} = 2\)
\(\Leftrightarrow \dfrac{x_1^2+x_2^2}{x_1^2x_2^2} = 2\) \(\Leftrightarrow \dfrac{x_1^2+x_2^2}{x_1^2x_2^2} = 2\) \(\Leftrightarrow \dfrac{(x_1+x_2)^2-2x_1x_2}{x_1^2x_2^2} = 2\)
\(\Leftrightarrow \dfrac{4^2-2m}{m^2} = 2\) (đkxđ \(m \leq 4; m ≠ 0 \)
)\(\Rightarrow 2m^2 +2m - 16 = 0\)
\(\Leftrightarrow \left[ \matrix{ m = \dfrac{-1+\sqrt{33}}{2} \hfill \cr m = \dfrac{-1-\sqrt{33}}{2} \hfill \cr} \right.\) (thoả mãn đk)
Kết luận.....
b/
Gọi số đó là \(\overline{AB}\) (A,B ∈ ℕ; A,B ≤ 9)
Theo bài ra ta có:
\(\left\{ \matrix{ A-B =2 \hfill \cr \overline{BA} = \dfrac{4}7.\overline{AB} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ A-B =2 \hfill \cr 10B + A = \dfrac{4}7.(10A+B) \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ A=4 \hfill \cr B=2 \hfill \cr} \right.\)
KL: số cần tìm là 42.
Câu 19: (2,5 điểm)
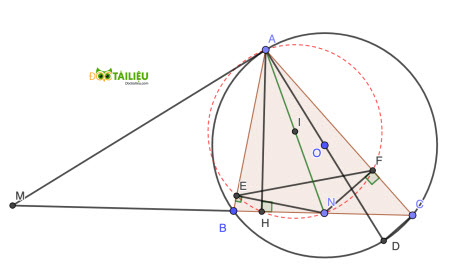
a)
Xét △MBA và △MAC có:
∠AMB chung
∠MAB = ∠ACB (t/c góc tạo bởi tiếp tuyến và dây cung)
Suy ra △MBA ∽ △MAC ⇒ \(\dfrac{MA}{MB} = \dfrac{MC}{MA}\) ⇒ MA² = MB.MC (đpcm).
b)
Từ A kẻ đường kính AD của (O).
Xét △ABH và △ADC có:
∠AHB = ∠ACD = 90°
∠ABH = ∠ABC = ∠ADC (góc nội tiếp (O) cùng chắn cung AC)
Suy ra △ABH ∽ △ADC ⇒ \(\dfrac{AB}{AH} = \dfrac{AD}{AC}\) ⇒ AB.AC = AD.AH = 2R.AH (đpcm).
c)
Gọi I là trung điểm AN.
Ta có: ∠AEN = ∠AHN = ∠AFN = 90° ⇒ E,H,F cùng thuộc đường tròn đường kính AN có I là tâm đường tròn.
Xét đường tròn (I; IN) ta có ∠EIF = 2.∠EAF (tính chất góc nội tiếp) = 2.∠BAC
Suy ra \( \dfrac{∠EIF}{2} = ∠BAC\) \(=const\).
Do IE = IF = AN/2 nên △IEF cân tại I ⇒ \(EF = 2 .IE.sin \space \dfrac{∠EIF}{2}\) \(= AN . sin \space \dfrac{∠EIF}{2}\)
Ta lại có AH ⊥ BC ⇒ \(AN \geq AH\)
⇒ \(EF = AN . sin \space \dfrac{∠EIF}{2} \geq AH. sin \space \dfrac{∠EIF}{2} \) \(=const\)
Vậy độ dài EF nhỏ nhất khi \(EF = AH. sin \space \dfrac{∠EIF}{2} \) ⇔ N trùng H.
Câu 20: (0,5 điểm)
Ta có: \(x^4-16x^2+32 = 0\)
\(\Leftrightarrow \left[ \matrix{ x^2 = 8+4\sqrt 2 \hfill \cr x^2 = 8-4\sqrt 2\hfill \cr} \right.\) (1) (cả 2 nghiệm đều \(>0\) nên thoả mãn)
Ta có:
\(x^2 = \left( \sqrt{6 - 3 \sqrt{2+ \sqrt 3}} - \sqrt{2 + \sqrt{2+ \sqrt 3}} \right)^2\)
\(=6 - 3 \sqrt{2+ \sqrt 3} + 2 + \sqrt{2+ \sqrt 3} -2 \sqrt{6 - 3 \sqrt{2+ \sqrt 3}}. \sqrt{2 + \sqrt{2+ \sqrt 3}} \)
\(=8 - 2 \sqrt{2+ \sqrt 3} -2 \sqrt{12 - 3 (2+ \sqrt 3)} \)
\(=8 - 2 \sqrt{2+ \sqrt 3} -2 \sqrt{6-3 \sqrt 3} \)
\(=8 - \sqrt{8+ 4\sqrt 3} - \sqrt{24-12 \sqrt 3} \)
\(=8 - \sqrt{(\sqrt 2+ \sqrt 6)^2} - \sqrt{(3\sqrt 2 - \sqrt 6)^2}\)
\(=8 - (\sqrt 2+ \sqrt 6) - (3\sqrt 2 - \sqrt 6)\)
\(=8 - 4\sqrt 2 \) (2)
Từ (1) và (2) suy ra \(x = \sqrt{6 - 3 \sqrt{2+ \sqrt 3}} - \sqrt{2 + \sqrt{2+ \sqrt 3}}\) là một nghiệm của phương trình đã cho (đpcm)
Trên đây là lời giải chi tiết đề kiểm tra học kì 2 môn Toán lớp 9 huyện Phú Mỹ năm học 2019/2020 mà các em có thể tham khảo, và là cơ sở giúp các em ôn tập chuẩn bị cho kì thi vào 10 sắp tới, các em cũng đừng quên tham khảo đề thi thử tuyển sinh vào lớp 10 tất cả các môn với trọn bộ đề thi của các trường trên cả nước nhé!
