Đọc Tài Liệu xin gửi tới các em đề thi tuyển sinh vào lớp 10 môn toán chung dành cho lớp chuyên tự nhiên năm học 2024 - 2025 trường THPT chuyên Lê Hồng Phong (Nam Định) được cập nhật nhanh nhất!
Đề 1 thi vào lớp 10 (TN) Lê Hồng Phong 2024
Sẽ cập nhật ngay sau khi kì thi diễn ra vào sáng ngày 24/5/2024 tại trường!

Gợi ý đáp án






Đề 1 thi vào 10 chuyên Tự nhiên Lê Hồng Phong 2023
Sẽ cập nhật ngay sau khi kì thi diễn ra vào sáng ngày 26/5/2023 tại trường!

Đáp án
(Đáp án dưới đây chỉ mang tính chất tham khảo, Đọc tài liệu sẽ cập nhật chi tiết đáp án và thang điểm chính thức khi trường công bố)!
Câu 1:

Câu 2:

Câu 3:

Câu 4:


Câu 5:


Tham khảo thêm các đề thi chính thức của các năm trước:
Đề 1 thi vào 10 chuyên Lê Hồng Phong Nam Định 2022

Đáp án đề tuyển sinh vào 10 môn Toán chung chuyên tự nhiên LHP
Câu 1

Câu 2

Câu 3.
1.

2.
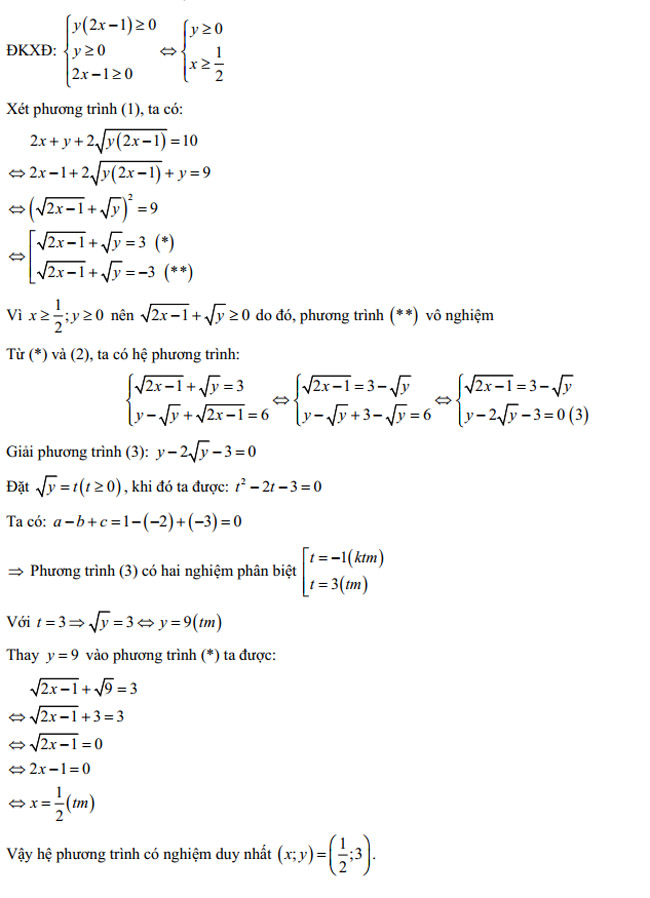
Câu 4.
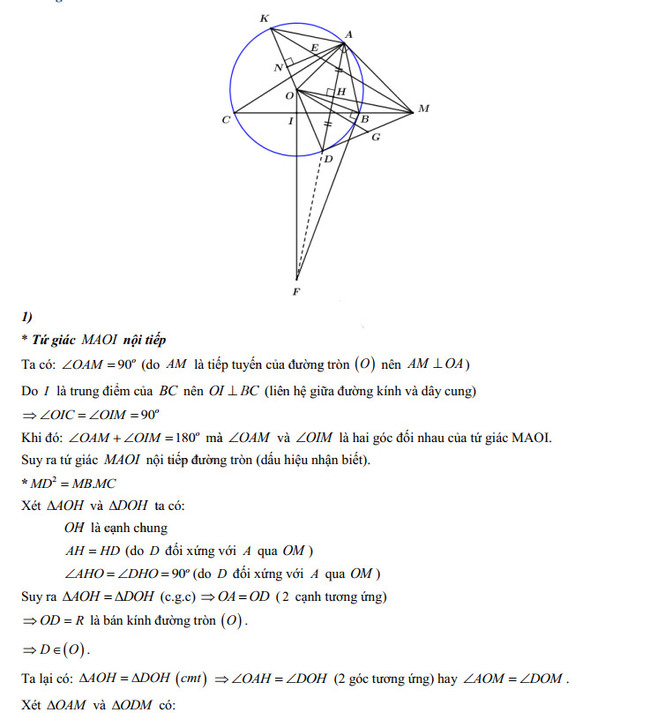

Câu 5.

Đề thi Toán vào lớp 10 Lê Hồng Phong Nam Định 2021 đề 1lớp chuyên tự nhiên

Đáp án đề thi môn toán lớp 10 (đề 1) chuyên Lê Hồng Phong Nam Định 2021
Câu 1.
1)
\(\begin{aligned} &\text { Biểu thức } P=\sqrt{\frac{x^{2}+1}{5 x-1}} \text { xác định khi và chi khi }\left\{\begin{array}{l} \frac{x^{2}+1}{5 x-1} \geq 0 \\ 5 x-1 \neq 0 \end{array} \Leftrightarrow 5 x-1>0 \Leftrightarrow x>\frac{1}{5} \text { (do } x^{2}+1 \geq 1>0 \forall x\right. \text { ). }\\ &\text { Vậy biểu thức } P=\sqrt{\frac{x^{2}+1}{5 x-1}} \text { xác định khi } x>\frac{1}{5} \text { . } \end{aligned}\)
2)
Đường thẳng \(y=m^{2} x+m-1(m \neq 0)\) và y=9x+2 song song với nhau khi và chỉ khi:
\(\left\{\begin{array} { l } { m ^ { 2 } = 9 } \\ { m - 1 \neq 2 } \end{array} \Leftrightarrow \left\{\begin{array}{l} m=\pm 3 \\ m \neq 3 \end{array} \Leftrightarrow m=-3\right.\right.\)
Vậy m=-3.
3)
Gọi H là trung điểm của BC
\(\Rightarrow B H=C H=\dfrac{1}{2} B C=\dfrac{1}{2} 2 \sqrt{3}=\sqrt{3}\)(cm).
Vì \(\triangle A B C \)đều nên \(A H \perp B C\) (trung tuyến đồng thời là đường cao).
Áp dụng định lí Pytago trong tam giác vuông A B H ta có
\(\begin{aligned} & A H^{2}=A B^{2}-B H^{2} \\ \Rightarrow & A H^{2}=(2 \sqrt{3})^{2}-(\sqrt{3})^{2} \\ \Rightarrow & A H^{2}=12-3=9 \\ \Rightarrow & A H=\sqrt{9}=3(cm) \end{aligned}\)
Vậy \(S_{\mathrm{MBC}}=\frac{1}{2} A H \cdot B C=\frac{1}{2} \cdot 3 \cdot 2 \sqrt{3}=3 \sqrt{3}\left(cm^{2}\right)\)
4)
Hinh nón đã cho có đường sinh l = 5 cm và bán kính đáy R=3 cm .
Chiều cao của hình nón là:
\(h=\sqrt{l^{2}-R^{2}}=\sqrt{5^{2}-3^{2}}=\sqrt{16}=4(cm).\)
Vậy thể tích khối nón là
\(V=\dfrac{1}{3} \pi R^{2} h=\dfrac{1}{3} \pi \cdot 3^{2} \cdot 4=12 \pi\left(\mathrm{cm}^{2}\right).\)
Đang cập nhật
Trên đây là toàn bộ nội dung của đề thi vào 10 toán chung dành cho khối tự nhiên được Đọc Tài Liệu chia sẻ.
Xem thêm đề thi các năm trước:
Đề toán chung Lê Hồng Phong năm 2020: Cả 2 đề 1 và 2.

Chi tiết trong: Đề thi tuyển sinh vào lớp 10 môn Toán chung năm 2020 Chuyên Lê Hồng Phong
Đề toán chung Lê Hồng Phong năm 2019

Chi tiết có trong: Đề thi Toán chung (đề 1) vào lớp 10 THPT Chuyên Lê Hồng Phong
Đề toán chung Lê Hồng Phong năm 2018:

Chi tiết tại: Đáp án đề thi môn toán lớp 10 chuyên Lê Hồng Phong Nam Định 2018
Đề toán chung Lê Hồng Phong năm 2017:

Chi tiết tại: Đề thi tuyển sinh vào 10 Toán chung 2017 chuyên Lê Hồng Phong
Đề Toán chuyên vào 10 Chuyên Lê Hồng Phong năm 2020 >> Tại đây
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình. Chúc các em hoàn thành bài thi môn toán lớp 10 (đề 1) chuyên Lê Hồng Phong Nam Định thật tốt.
Tham khảo thêm:
