Đáp án đề thi học kì 1 môn Toán 9 tỉnh Bến Tre năm 2020/2021

Cùng Đọc Tài Liệu tham khảo đáp án đề thi học kì 1 Toán lớp 9 của tỉnh Bến Tre dưới đây bạn nhé:

Đề thi học kì 1 môn Toán 9 tỉnh Bến Tre năm 2020

Câu 1 (2,5 diểm)

a) Tìm điều kiện xác định của biều thức: \(\sqrt{2 x-4}\).

b) Rút gọn các biểu thức sau:

\(A=(5 \sqrt{2}-\sqrt{32}): \sqrt{2} \)

\(B=\sqrt{(\sqrt{3}-2)^{2}}+\sqrt{(\sqrt{3}+\sqrt{2})^{2}}\)

\(C=\frac{a-b}{\sqrt{a}-\sqrt{b}}-\sqrt{a} \) với \(a \geq 0, b \geq 0, a \neq b\)

Câu 2 (2,0 diểm) Cho hàm số y = 3x - 5 có đồ thị (d).

a) Hàm số trên là hàm số nghịch biến hay đồng biến? Vì sao?

b) Tìm m để (d) song song với đường thẳng y = (2m-1)x + 1

c) Vẽ (d) trên mặt phằng tọa độ (Oxy).

Câu 3 (1,5 diểm) Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC). Biết AB = 6 cm, BC = 10 cm

a) Tính AC, cos B.

b) Tinh số đo góc BAH.

Câu 4 (0,5 điểm) 

Tích cực thực hiện “5K: Khẩu trang - Khử khuẩn – Khoảng cách – Không tập trung - Khai bảo y tế để giữ an toàn cho chúng ta trước đại dịch COVID-19, việc súc họng và miệng thường xuyên bằng nước muối sinh lý cũng có thể giúp chúng ta phòng ngừa dịch bệnh COVID-19. Nước muối sinh lý (hay còn được gọi là dung dịch Natri Clorid 0,9%) có thể được pha chế bằng cách hòa tan 9g muối ăn trong 1000ml nước (nước cất hoặc nước đã được xử lý bằng máy lọc hoặc nước đun sôi để nguội).

Để có nước muối sinh lý sử dụng mỗi ngày, bạn Bình đã pha 18g muối ăn vào 1800ml nước đun sôi để nguội. Hỏi bạn Bình pha chế đúng cách chưa? Bạn Bình cần phải pha thêm bao nhiêu ml nước đun sôi để nguội để có nước muối sinh lí ?

Câu 5 (3,5 điểm)

Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt BC tại D.

a) Chứng minh: AC² = CD.BC.

b) Gọi I là trung điểm của BD. Tiếp tuyến tại D của (O) cắt AC tại M và cắt OI tại N. Chứng minh: NB là tiếp tuyến của (O).

c) OM cắt AD ở K. Chứng minh: OK.OM = OI.ON.

-Hết-

Đáp án đề thi học kì 1 môn Toán 9 tỉnh Bến Tre năm 2020

Câu 1 (2,5 diểm)

a) ĐKXĐ: x ≥ 2 .

b)

\(A=(5 \sqrt{2}-\sqrt{32}): \sqrt{2} \) = \((5 \sqrt{2}-4\sqrt{2}): \sqrt{2} \) = 1

KL: ...

\(B=\sqrt{(\sqrt{3}-2)^{2}}+\sqrt{(\sqrt{3}+\sqrt{2})^{2}}\) = \(2 - \sqrt{3} +\sqrt{3}+\sqrt{2}\) = \(2 +\sqrt{2}\)

KL: ..

\(C=\frac{a-b}{\sqrt{a}-\sqrt{b}}-\sqrt{a} \) với \(a \geq 0, b \geq 0, a \neq b\)

⇔ \(C=\frac{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}{\sqrt{a}-\sqrt{b}}-\sqrt{a} \) = \(\sqrt{a}+\sqrt{b}-\sqrt{a} \) = \(\sqrt{b}\)

KL: ..

Câu 2 (2,0 diểm)

a) Hàm số trên có hệ số góc m = 3 > 0 ⇒ hàm số là đồng biến trên ℝ.

b) Để (d) song song với đường thẳng y = (2m-1)x + 1 khi và chỉ khi:

\(\left\{ \matrix{ 3 = 2m-1 \hfill \cr -5 ≠ 1 \hfill \cr} \right.\)

⇒ m = 2.

KL: ..

c) Vẽ (d) trên mặt phằng tọa độ (Oxy).

Câu 3 (1,5 diểm) 

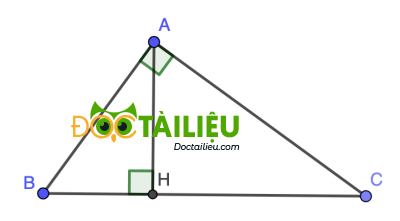
a)

Áp dụng Pytago ta có:

\(AC = \sqrt{{BC}^2 - {AB}^2} = \sqrt{{10}^2 - {6}^2} = 8\) (cm)

\(cos B = \dfrac{AB}{BC}=\dfrac{3}5\)

KL: ..

b)

Ta có:

\(sin∠ BAH = sin (90° - B) = cos B = \dfrac{3}5\)

⇒ \(∠ BAH ≈ 36,87°\)

KL: ..

Câu 4 (0,5 điểm) 

Nồng độ nước muối ban đầu của Bình là: \(\dfrac{18}{1800} = 1\%\) ≠ 0,9%

⇒ Bạn Bình pha chế chưa đúng.

Số ml nước sôi để nguội cần pha thêm là:

\(\dfrac{18} {0,9 \% } - 1800 = 200\) (ml)

KL: ..

Câu 5 (3,5 điểm)

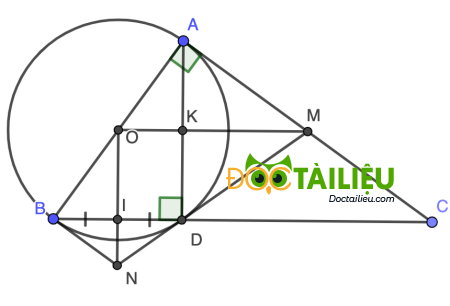
a)

Vì D thuộc đường tròn đường kính AB ⇒ ∠BDA = 90° = ∠CDA.

Xét △CAD và △CBA, ta có:

\(\left\{ \matrix{ \text{góc C chung} \hfill \cr ∠CDA = ∠CAB = 90° \hfill \cr} \right.\)

Suy ra △CAD ∽ △CBA (g.g) ⇒ \(\dfrac{CA}{CB} = \dfrac{CD}{CA} \)

⇒ AC² = CD.BC (đpcm)

b)

Dễ thấy OB = OD = R, I là trung điểm BD ⇒ OI là đường trung trực của BD

⇒ ∠OBN = ∠ODN.

Lại có MN là tiếp tuyến tại D của (O) ⇒ OD ⊥ MN tại D hay ∠ODN = 90° = ∠OBN

Suy ra BN là tiếp tuyến tại B của (O) (đpcm).

c)

Xét △ODI và △OND, ta có:

\(\left\{ \matrix{ \text{góc NOD chung} \hfill \cr ∠OID = ∠ODN = 90° \hfill \cr} \right.\)

Suy ra △ODI ∽ △OND (g.g) ⇒ \(\dfrac{OD}{OI} = \dfrac{ON}{OD} \)

⇒ OD² = ON.OI (1)

Tương tự, xét △ODK và △OMD, ta có:

\(\left\{ \matrix{ \text{góc MOD chung} \hfill \cr ∠OKD = ∠ODM = 90° \hfill \cr} \right.\)

Suy ra △ODK ∽ △OMD (g.g) ⇒ \(\dfrac{OD}{OK} = \dfrac{OM}{OD} \)

⇒ OD² = OM.OK (2)

Từ (1) và (2) suy ra OM.OK = ON.OI (đpcm).

-/-

Trên đây là đề thi học kì 1 Toán 9 tỉnh Bến Tre năm 2020/2021 do Đọc tài liệu thực hiện, mong rằng với nội dung này sẽ giúp các em ôn tập kiến thức thi cuối kì 1 tốt hơn. Đừng quên còn trọn bộ đề thi thử vào 10 môn Toán qua các năm đang đợi các em giải đáp.