Cùng Đọc Tài Liệu tham khảo đáp án đề thi học kì 1 Toán lớp 9 của trường chuyên Ams dưới đây bạn nhé:
Đề thi

Đề thi học kì 1 môn Toán 9 chuyên Amsterdam năm 2020 thi trong thời gian 90 phút với 4 bài đều thuộc kiến thức học kì 1 môn Toán 9. Đề thi gồm 3 câu hỏi đại số và 1 câu hỏi hình trong, trong đó ý c, d bài 3 và ý b bài 4 là câu hỏi khá giỏi kiếm điểm 10, cùng Đọc tài liệu giải bài tập này bạn nhé:
Đáp án đề thi học kì 1 môn Toán 9 chuyên Amsterdam năm 2020
Bài 1:
\(A=\dfrac{5}{\sqrt{x}+2}-\dfrac{2 \sqrt{x}-11}{x-4}+\dfrac{2}{2-\sqrt{x}} \) và \(B=\dfrac{x-4}{\sqrt{x}}\) (với x > 0, x ≠ 4)
a, Với x = 16, ta có:
\(B=\dfrac{x-4}{\sqrt{x}} = \dfrac{16-4}{\sqrt{16}} = \dfrac{12}4 = 3\)
b,
ĐKXĐ: x > 0, x ≠ 4, ta có:
\(A=\dfrac{5}{\sqrt{x}+2}-\dfrac{2 \sqrt{x}-11}{x-4}+\dfrac{2}{2-\sqrt{x}} \)
\(=\dfrac{5}{\sqrt{x}+2}-\dfrac{2 \sqrt{x}-11}{(\sqrt{x}+2)(\sqrt{x}-2)}+\dfrac{2}{2-\sqrt{x}} \)
\(=\dfrac{5(\sqrt{x}-2) - 2 \sqrt{x}+11 - 2(\sqrt{x}+2)}{(\sqrt{x}+2)(\sqrt{x}-2)}\)
\(=\dfrac{\sqrt{x}-3}{(\sqrt{x}+2)(\sqrt{x}-2)}\)\(=\dfrac{\sqrt{x}-3}{x-4}\)
KL...
c,
ĐKXĐ: x > 0, x ≠ 4, ta có:
\(C=\dfrac{x+2 \sqrt{x}+4}{x-4} \cdot B\)
\(=\dfrac{x+2 \sqrt{x}+4}{x-4} \cdot \dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{x+2 \sqrt{x}+4}{\sqrt{x}}\)
\(=\sqrt{x} + \dfrac{4}{\sqrt{x}} + 2\)
Áp dụng AM-GM, ta có:
\(\sqrt{x} + \dfrac{4}{\sqrt{x}} \geq 2\sqrt{\sqrt{x} . \dfrac{4}{\sqrt{x}}} = 4\)
\(\Leftrightarrow C =\sqrt{x} + \dfrac{4}{\sqrt{x}} + 2 \geq 4 + 2 = 6\)
\(\Leftrightarrow C \geq 6\) mà x > 0, x ≠ 4
⇔ Để C đạt giá trị nhỏ nhất là số nguyên ⇔ C = 7 ⇔
\(C = \sqrt{x} + \dfrac{4}{\sqrt{x}} + 2 = 7\)
\(\Leftrightarrow \sqrt{x} + \dfrac{4}{\sqrt{x}} - 5 = 0\)
\(\Leftrightarrow x - 5\sqrt{x} +4 = 0\)
\(\Leftrightarrow \left[ \matrix{ \sqrt x = 4 \hfill \cr \sqrt x = 1 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ x = 16 \hfill \cr x = 1 \hfill \cr} \right.\) (tm đkxđ)
KL....
Bài 2:
a, Với m = 2, ta có:
(d): y = x + 2
Khoảng cách từ O tới (d) là:
\(d(O,d) = \dfrac{|1.0 - 1.0 + 2|}{\sqrt{1^2+1^2}} = \dfrac{2}{\sqrt{2}} = \sqrt{2}\)
KL...
b,
Xét phương trình hoành độ giao điểm của (d) và (d'), ta có:
\((m-1)x + m = -2x + m^2 - 2\) (1)
Để (d) cắt (d') tại 1 điểm trên trục tung ⇔ (1) có nghiệm x = 0
⇔ \((m-1).0 + m = -2.0 + m^2 - 2\)
⇔ \(m^2-m - 2 = 0\)
\(\Leftrightarrow \left[ \matrix{ m = -1 \hfill \cr m = 2 \hfill \cr} \right.\)
(tm)KL...
c, Để thoả mãn yêu cầu đề bài thì
\(d(O,d) = \dfrac{1}{\sqrt{5}} = \dfrac{|m|}{\sqrt{(m-1)^2 + 1^2}}\) (đk m ≠ 0)
\(\Leftrightarrow \dfrac{(m-1)^2 + 1^2}{m^2}=5\)
\(\Leftrightarrow 4m^2+2m -2 = 0\)
\(\Leftrightarrow \left[ \matrix{ m = -1 \hfill \cr m = \dfrac{1}2 \hfill \cr} \right.\) (tm đkxđ)
KL...
Bài 3:
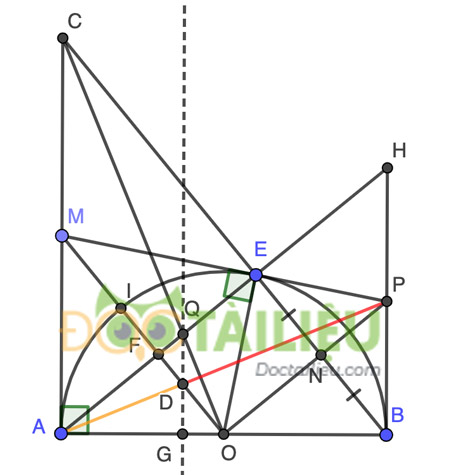
Hình ảnh của bài 3 - Đáp án đề thi học kì 1 môn Toán 9 chuyên Amsterdam năm 2020
a, Vì E đối xứng với A qua OM ⇒ OA = OE và MA = ME.
Xét 2 △OMA và △OME, ta có:
\(\left\{ \matrix{ OA = OE \hfill \cr MA = ME \hfill \cr \text{Cạnh OM chung} \hfill \cr} \right.\) ⇒ △OMA ~ △OME (c.c.c)
⇒ ∠MEO = ∠MAO = 90° hay ME ⊥ EO hay ME là tiếp tuyến của nửa đường tròn (O) (đpcm).
b, Dễ thấy OM ⊥ AE nên I là điểm chính giữa cung AE
⇒ ∠IAE = ∠IBE = ∠IBA = ∠IAM (tính chất góc tạo bởi tiếp tuyến và dây cung, dây cung bằng nhau)
⇒ AI là tia phân giác của ∠MAE (1)
Từ phần A có ∠AMI = ∠EMI ⇒ MI là tia phân giác của ∠AME (2)
Từ (1) và (2) suy ra I là tâm đường tròn nội tiếp △AME (đpcm).
c, Gọi OM cắt AE tại F. Dễ thấy ONEF là hình chữ nhật ⇒ ∠MOP = 90°.
Xét △OEM và △PEO, ta có:
\(\left\{ \matrix{ ∠OEM = ∠PEO = 90° \hfill \cr ∠EMO = ∠EOP \text{ (cùng = 90° - ∠MOE)} \hfill \cr} \right.\) ⇒ △OEM ~ △PEO (g.g)
⇒ \(\dfrac{OE}{ME} = \dfrac{PE}{OE}\) ⇔ \({OE}^2 = PE.ME = R^2\)
Áp dụng BĐT AM GM ta có:
\(MP = ME + PE \geq 2\sqrt{ME.PE} = 2R \)
Ta lại có: \(S_{\triangle MOP} = \dfrac{1}2OE.MP \geq \dfrac{1}2 R.2R\)
\(\Leftrightarrow S_{\triangle MOP} \geq R^2\)
Vậy min \( S_{\triangle MOP} = R^2\) \(\Leftrightarrow ME = PE \) hay AMEO là hình vuông hay AM = AO = R.
KL..
d, Kéo dài QD cắt AB tại G, AE cắt PB tại H.
Ta thấy △AEC vuông tại E, có AM = ME ⇒ M là trung điểm AC ⇒ MA = MC.
Tương tự ta có P là trung điểm HB của △HEB vuông tại E ⇒ PH = PB.
Từ phần c, ta có ∠OEP = ∠OBP = 90° ⇒ BH // AC.
Áp dụng Thales cho 2 đường song song QG và CA ta có:
\(\dfrac{QD}{CM} = \dfrac{OD}{OM} = \dfrac{DG}{MA}\)
Mà MA = MC (cmt) ⇒ QD = DG (3)
Gọi AP cắt QG tại D', áp dụng Thales cho QG và HB ta có:
\(\dfrac{QD'}{HP} = \dfrac{AD'}{AP} = \dfrac{D'G}{PB}\)
Mà PH = PB (cmt) ⇒ QD' = D'G (4)
Từ (3) và (4) ⇒ D ≡ D' hay 3 điểm A D P thẳng hàng (đpcm).
Bài 4:
a, ĐKXĐ: \(x \geq \dfrac{-1}2\)
Ta có:
\(x^2 - 1 = 2\sqrt{2x+1}\)
\(\Leftrightarrow x^2 + 2x = 2\sqrt{2x+1} + 2x + 1\)
\(\Leftrightarrow x^2 + 2x + 1 = 2x + 1 + 2\sqrt{2x+1} + 1\)
\(\Leftrightarrow (x+1)^2 = (\sqrt{2x+1} + 1)^2\)
\(\Leftrightarrow \left[ \matrix{ x+1 = \sqrt{2x+1}+1 \hfill \cr x+1 = -\sqrt{2x+1}-1 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ x= \sqrt{2x+1}\hfill \cr x+2 = -\sqrt{2x+1} \leq 0 \hfill \cr} \right.\)
Vì \(x \geq \dfrac{-1}2\) \(\Leftrightarrow x + 2 > 0\) với mọi x, mâu thuẫn với phương trình (2) nên ta có:
\(x= \sqrt{2x+1}\) (ĐKXĐ \(x \geq 0\))
\(\Leftrightarrow x^2 - 2x - 1 = 0\)
\(\Leftrightarrow \left[ \matrix{ x=1+\sqrt 2 \space \text {(tm)}\hfill \cr x=1-\sqrt 2 \space \text {(loại vì x ≥ 0)}\hfill \cr} \right.\)
KL...
b, Với a, b > 0 ta có:
\(a-\sqrt{a}=\sqrt{b}-b\)
\(\Leftrightarrow a + b = \sqrt{b} + \sqrt{a}\)
Áp dụng BĐT Bunhia Copxki ta có:
\(a^2 + b^2 \geq \dfrac{(a+b)^2}{2}\)
\(\Leftrightarrow P=a^{2}+b^{2}+\dfrac{2020}{(\sqrt{a}+\sqrt{b})^{2}} \geq \dfrac{(a+b)^2}{2} + \dfrac{2020}{(\sqrt{a}+\sqrt{b})^{2}} \)
\(\Leftrightarrow P\geq \dfrac{(a+b)^2}{2} + \dfrac{2020}{(a+b)^{2}} \) (vì \(a + b = \sqrt{b} + \sqrt{a}\))
Áp dụng BĐT AM GM ta có:
\(P\geq \dfrac{(a+b)^2}{2} + \dfrac{2020}{(a+b)^{2}} \geq 2\sqrt{\dfrac{2020}2}= 2\sqrt{1010}\)
Vậy \(min_P = 2\sqrt{1010}\) \(\Leftrightarrow a=b\).
Mong rằng với đáp án đề thi học kì 1 môn Toán 9 chuyên Amsterdam năm 2020 sẽ là một tài liệu ôn thi thuận tiện với các câu hỏi và các dạng đề Toán thường được ra trong học kì 1, đừng quên có rất nhiều các đề thi thử vào 10 môn Toán của các trường trên cả nước đợi em thử sức đó nhé!
