Câu hỏi ôn tập chương 1 đại số 6 tập 1 trang 61

Đề bài:

Câu 1: Viết dạng tổng quát các tính chất giao hoán, kết hợp của phép cộng, phép nhân, tính chất phân phối của phép nhân đối với phép cộng.

Câu 2: Lũy thừa bậc n của a là gì?

Câu 3: Viết công thức nhân hai lũy thừa cùng cơ số, chia hai lũy thừa cùng cơ số.

Câu 4:

Khi nào ta nói số tự nhiên a chia hết cho số tự nhiên b.

Câu 5: Phát biểu và viết dạng tổng quát hai tính chất chia hết của một tổng.

Câu 6: Phát biểu các dấu hiệu chia hết cho 2, cho 3, cho 5, cho 9.

Câu 7: Thế nào là số nguyên tố, hợp số ? Cho ví dụ.

Câu 8: Thế nào là hai số nguyên tố cùng nhau ? Cho ví dụ.

Câu 9: ƯCLN của hai hay nhiều số là gì ? Nêu cách tìm.

Câu 10: BCNN của hai hay nhiều số là gì ? Nêu cách tìm.

Đáp án:

Câu 1:

Phép tính	Cộng	Nhân
Giao hoán	a + b = b + a	a.b = b.a
Kết hợp	(a + b) + c = a + (b + c)	(a.b).c = a.(b.c)
Phân phối	a(b + c) = ab + ac

Câu 2:

Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:

Câu 3: 

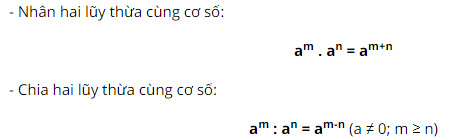
Câu 4: 

Số tự nhiên a chia hết cho số tự nhiên b khác 0 nếu có số tự nhiên k sao cho a = b.k.

Kí hiệu: a ⋮ b

Câu 5:

- Tính chất 1: a ⋮ m và b ⋮ m => (a + b) ⋮ m

Tổng quát: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

a ⋮ m, b ⋮ m và c ⋮ m => (a + b + c) ⋮ m

- Tính chất 2: a :/. m và b ⋮ m => (a + b) :/. m

Tổng quát: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.

a :/. m, b ⋮ m và c ⋮ m => (a + b + c) :/. m

Câu 6:

- Dấu hiệu chia hết cho 2: Các số có chữ số tận cùng là chữ số chẵn thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

- Dấu hiệu chia hết cho 3: Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

- Dấu hiệu chia hết cho 5: Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

- Dấu hiệu chia hết cho 9: Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

Câu 7:

- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Ví dụ: 2, 3, 5, 7, 11, ...

- Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.

Ví dụ: 4, 6, 8, 9, ...

Câu 8:

- Hai số có ƯCLN bằng 1 gọi là các số nguyên tố cùng nhau.

Ví dụ: 8 và 9 là hai số nguyên tố cùng nhau.

Câu 9:

- ƯCLN của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

- Cách tìm:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó. Tích đó là ƯCLN phải tìm.

Câu 10:

- BCNN của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

- Cách tìm:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.