Đề bài
Tìm số giao điểm của đường thẳng d và mặt phẳng (α):
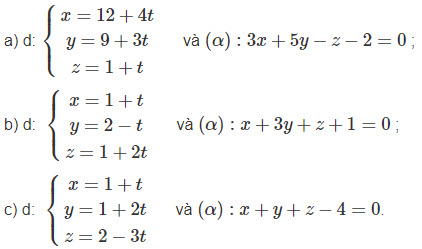
Hướng dẫn giải
Phương pháp tìm giao điểm của đường thẳng d : 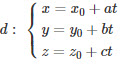 ( t ∈ R ) và mặt phẳng ( P ) : Ax + By + Cz + D = 0 .
( t ∈ R ) và mặt phẳng ( P ) : Ax + By + Cz + D = 0 .
Gọi M = d ∩ ( P ) ⇒ M ∈ d ⇒ M ( x₀ + at ; y₀ + bt ; z₀ + ct ) .
Thay tọa độ điểm M vào phương trình mặt phẳng (P), tìm ẩn t, sau đó suy ra tọa độ điểm M .
Đáp án bài 5 trang 90 sgk Hình học lớp 12
a) Gọi M = d ∩ ( α ) ⇒ M ∈ d ⇒ M ( 12 + 4 t ; 9 + 3 t ; 1 + t ) . Vì M ∈ ( α ) nên ta có:
3 ( 12 + 4t ) + 5 ( 9 + 3t ) − ( 1 + t ) − 2 = 0
⇔ 26t + 78 = 0 ⇔ t = − 3 .
Vậy d ∩ ( α ) = M ( 0;0 ; − 2 ) .
b) Gọi M = d ∩ ( α ) ⇒ M ∈ d ⇒ M ( 1 + t ; 2 − t ; 1 + 2t ) . Vì M ∈ ( α ) nên ta có:
( 1 + t ) + 3. ( 2 − t ) + ( 1 + 2t ) + 1 = 0
⇔ 0.t + 9 = 0 , phương trình vô nghiệm.
Chứng tỏ d và ( α ) không cắt nhau hay d // ( α ) .
c) Gọi M = d ∩ ( α ) ⇒ M ∈ d ⇒ M ( 1 + t ; 1 + 2 t ; 2 − 3 t ) . Vì M ∈ ( α ) nên ta có: ( 1 + t ) + ( 1 + 2t ) + ( 2 − 3t ) − 4 = 0
⇔ 0t + 0 = 0
Phương trình này có vô số nghiệm, chứng tỏ d ⊂ (α).
Trên đây là lời giải bài tập số 5 trang 90, các bạn có thể tham khảo thêm đáp án Bài 6 tr. 61 sgk Hình học 12 tại doctailieu.com.