Bạn muốn giải bài 38 trang 129 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 chương 4 phần hình học để tự tin giải tốt các bài tập khác trong tiết ôn tập chương 4 hình trụ, hình nón và hình cầu.
Đề bài 38 trang 129 SGK Toán 9 tập 2
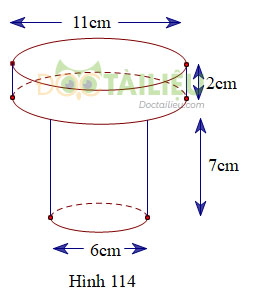
Hãy tính thể tích , diện tích bề mặt một chi tiết máy theo kích thước đã cho trên hình 114.
» Bài tập trước: Bài 37 trang 126 SGK Toán 9 tập 2
Giải bài 38 trang 129 SGK Toán 9 tập 2
Hướng dẫn cách làm
+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)
+) Diện tích toàn phần của hình trụ: \(S_{tp}=2 \pi rh +2 \pi r^2.\)
+) Thể tích hình trụ là: \(V=\pi r^2h.\)
Đáp án chi tiết
Dưới đây là các cách giải bài 38 trang 129 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:
* Ta có: Thể tích phần cần tính là tổng thể tích của hai hình trụ có đường kính là \(11cm\) và chiều cao là \(2cm\).
\(\displaystyle {V_1} = \pi {R^2}{h_1} = \pi {\left( {{{11} \over 2}} \right)^2}.2 = 60,5\pi \left( {c{m^3}} \right)\)
Thể tích hình trụ có đường kính đáy là \(6cm\), chiều cao là \(7cm\)
\(\displaystyle {V_2} = \pi {R^2}{h_2} = \pi {\left( {{6 \over 2}} \right)^2}.7 = 63\pi \left( {c{m^3}} \right)\)
Vậy thể tích của chi tiết máy cần tính là:
\(V = {V_1} + {V_2} = 60,5\pi + 63\pi = 123,5\pi (c{m^3})\)
* Tương tự, theo đề bài diện tích bề mặt của chi tiết máy bằng tổng diện tích xung quanh của hai chi tiết máy với diện tích 2 hình tròn đáy của hình trụ nằm trên.
Diện tích toàn phần của hình trụ có đường kính đáy \(11 cm\), chiều cao là \(2cm\) và là:
\({S_{tp(1)}} = 2\pi R_1{h_1} + 2\pi {R_1}^2 \)
\(\displaystyle = 2\pi {{11} \over 2}.2 + 2\pi .5,5^2 = 82,5 \pi \left( {c{m^2}} \right)\)
Diện tích xung quanh của hình trụ có đường kính đáy là \(6cm\) và chiều cao là \(7cm\) là:
\(\displaystyle {S_{xq(2)}} = 2\pi R_2 {h_2} = 2\pi {6 \over 2}.7 = 42\pi \left( {c{m^2}} \right)\)
Vậy diện tích bề mặt của chi tiết máy là:
\(S = {S_{tp(1)}} + {\rm{ }}{S_{xq(2)}} = 82,5\pi + 42\pi = 124,5\pi (c{m^2}).\)
» Bài tiếp theo: Bài 39 trang 129 SGK Toán 9 tập 2
Nội dung trên đã giúp bạn nắm được cách làm bài 38 trang 129 SGK Toán 9 tập 2. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.
